Cho A=2x2-5x;B=-x2+x+3;C=2x-2
Chứng minh rằng tring 3 biểu thức điA,B,C có ít nhất một biểu thức luôn có giá trị không âm với mọi giá trị của x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với x = 20040, ta có: A = 10/20040 = 1/2004.
Vậy A = 1/2004 khi x = 20040.

Với x = 20040, ta có: A = 10/20040 = 1/2004.
Vậy A = 1/2004 khi x = 20040.

Ta có: B . (2x2 – 5x + 1)
= (x2 – 4x – 3) . (2x2 – 5x + 1)
= x2 .(2x2 – 5x + 1) – 4x . (2x2 – 5x + 1) – 3.(2x2 – 5x + 1)
= x2 . 2x2 + x2 . (-5x) + x2 . 1 – [4x . 2x2 + 4x . (-5x) + 4x . 1] – [3.2x2 + 3.(-5x) + 3.1]
= 2x4 – 5x3 + x2 – ( 8x3 – 20x2 + 4x) – (6x2 – 15x + 3)
= 2x4 – 5x3 + x2 – 8x3 + 20x2 - 4x – 6x2 + 15x - 3
= 2x4 + (-5x3 – 8x3) + (x2 + 20x2 – 6x2 ) + (-4x + 15x) – 3
= 2x4 - 13x3 + 15x2 + 11x - 3
=A
Vậy ta có phép chia hết A : B = 2x2 – 5x + 1

Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
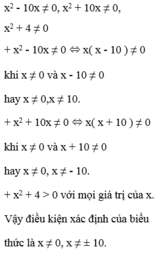

Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
