Cho (O), đường kính BC. A thuộc (O), AH vuông góc BC. (A;AH) cắt (O) tại D, E. DE cắt AO tại K.
a) Chứng minh: AD2=AK.AO
b) DE cắt AH tại I. Chứng minh: IA=IH.
Mọi người làm được câu nào thì giúp em nha.Em cần rất gấp và hạn nộp bài của em là trước 23:59 hôm nay ạ

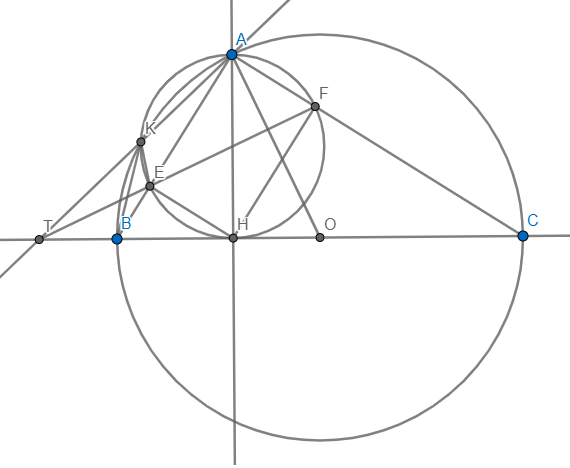
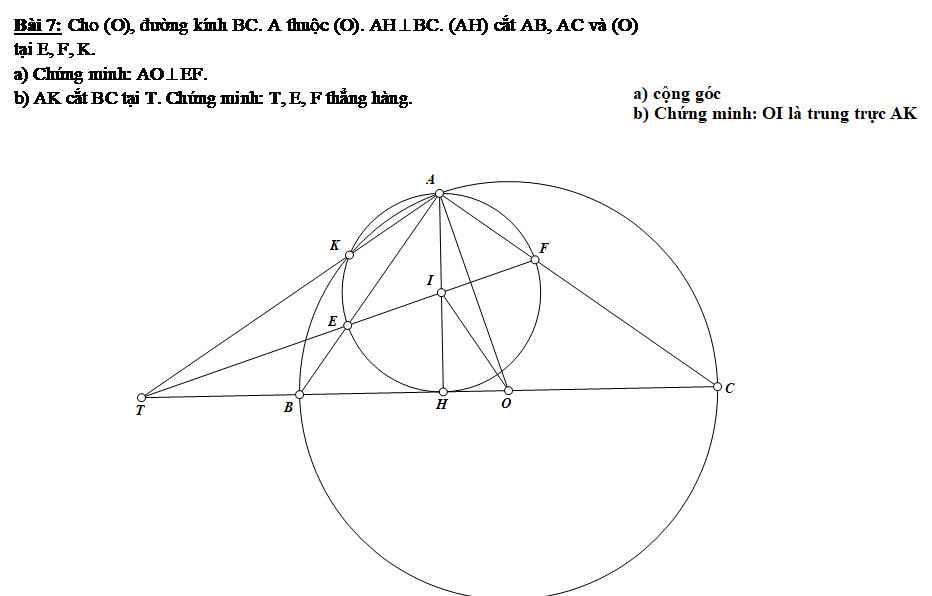

a) AO cắt (O) tại F \(\Rightarrow AF\) là đường kính \(\Rightarrow\angle ADF=90\)
Vì DE là dây chung của (A;AH) và (O) và AO là đường nối tâm
\(\Rightarrow AO\bot DE\)
Xét \(\Delta ADK\) và \(\Delta AFD:\) Ta có: \(\left\{{}\begin{matrix}\angle DAFchung\\\angle AKD=\angle ADF=90\end{matrix}\right.\)
\(\Rightarrow\Delta ADK\sim\Delta AFD\left(g-g\right)\Rightarrow\dfrac{AD}{AF}=\dfrac{AK}{AD}\Rightarrow AD^2=AF.AK\)
mà \(AF=2AO\Rightarrow AD^2=2AO.AK\)
b) Xét \(\Delta AIK\) và \(\Delta AOH:\) Ta có: \(\left\{{}\begin{matrix}\angle HAOchung\\\angle AKI=\angle AHO=90\end{matrix}\right.\)
\(\Rightarrow\Delta AIK\sim\Delta AOH\left(g-g\right)\Rightarrow\dfrac{AI}{AO}=\dfrac{AK}{AH}\Rightarrow AI.AH=AK.AO\)
\(\Rightarrow AI.AH=\dfrac{AD^2}{2}=\dfrac{AH^2}{2}\) (cùng = bán kính của (A;AH))
\(\Rightarrow AI=\dfrac{AH}{2}\Rightarrow I\) là trung điểm AH