Cho hình thoi ABCD, biết BD = 18dm ; AC = 25dm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Do \(ABCD\) là hình thoi nên hai đường chéo vuông góc với nhau tạo ra 4 góc vuông.
Áp dụng ĐL Pythagore vào 1 trong các tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{6}{2}} \right)}^2} + {{\left( {\frac{8}{2}} \right)}^2}} = \sqrt {9 + 16} = \sqrt {25} = 5\) (cm)
C
28 tháng 3 2022
Đường chéo ac là:
9:4x3=6,75 (cm)
Diện tích hình thoi là:
6,75x9:2=30,375(cm2)
Đáp số: 30,375 cm2
2 tháng 10 2021
Ta có: \(S_{ABCD}=\dfrac{1}{2}.BD.AC\)(với S là diện tích)
\(\Rightarrow\dfrac{1}{2}.2a.8a=32\)
\(\Rightarrow8a^2=32\)
\(\Rightarrow a^2=4\)
\(\Rightarrow a=2\left(cm\right)\)
CM
28 tháng 8 2017
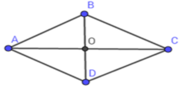
Ta có: AC = 2AO = 2.12 = 24cm
SABCD = 1 2 BD.AC
=> BD = 2 S A B C D A C = 2.168 24 =14(cm)
=> BO = 1 2 BD = 1 2 .14 = 7(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 12 2 + 7 2 = 193 (cm)
Đáp án cần chọn là: C
CM
5 tháng 11 2019
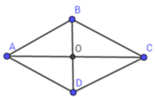
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A
CM
9 tháng 5 2017
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B