Tính giá trị biểu thức A biết \(cosx=0,5;A=\dfrac{cosx+2sin^2x}{cos^2x-sinx}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sin x+cosx=m
=>(sinx+cosx)^2=m^2
=>1+2*cosx*sinx=m^2
=>2*sinx*cosx=m^2-1
=>\(sinx\cdot cosx=\dfrac{m^2-1}{2}\)
\(sin^3x+cos^3x=\left(sinx+cosx\right)^3-3\cdot sinx\cdot cosx\cdot\left(sinx+cosx\right)\)\(=m^3-3\cdot\dfrac{m^2-1}{2}\cdot m\)
\(=m^3-\dfrac{3m^3-3m}{2}\)
\(=\dfrac{2m^3-3m^3+3m}{2}=\dfrac{-m^3+3m}{2}\)

Lần sau bạn vào cái hình E để gửi câu hỏi nha!
\(P=\dfrac{sin^2\alpha-sin\alpha\cdot cos\alpha+2cos^2\alpha}{2sin^2\alpha-cos^2\alpha}\)
\(P=\dfrac{tan^2\alpha-tan\alpha+2}{2tan^2\alpha-1}\) (Chia cả tử và mẫu cho \(cos^2\alpha\))
\(P=\dfrac{3^2-3+2}{2\cdot3^2-1}=\dfrac{8}{17}\)
Chúc bn học tốt!

\(tan^2x+cot^2x=2=2.tanx.cotx\)
\(\Leftrightarrow tan^2x+cot^2x-2tanx.cotx=0\)
\(\Leftrightarrow\left(tanx-cotx\right)^2=0\Leftrightarrow tanx=cotx=\dfrac{1}{tanx}\)
\(\Leftrightarrow tanx=\pm1\)
\(P=\dfrac{1}{cosx}-\dfrac{cosx}{1+sinx}=\dfrac{1+sinx-cos^2x}{cosx\left(1+sinx\right)}=\dfrac{sin^2x+sinx}{cosx\left(1+sinx\right)}\)
\(=\dfrac{sinx\left(1+sinx\right)}{cosx\left(1+sinx\right)}=tanx=\pm1\)

a: A=(sinx+cosx)^2-1=m^2-1
b: B=căn (sinx+cosx)^2-4sinxcosx=căn m^2-4(m^2-1)=căn -3m^2+4
c: C=(sin^2x+cos^2x)^2-2(sinx*cosx)^2=1-2m^2

1: \(P=sin^22x=1-cos^22x\)
\(=1-\left(cos2x\right)^2\)
\(=1-\left(2cos^2x-1\right)^2\)
\(=1-\left(2\cdot\dfrac{9}{16}-1\right)^2\)
\(=1-\left(\dfrac{9}{8}-1\right)^2=1-\left(\dfrac{1}{8}\right)^2=\dfrac{63}{64}\)
2:
\(cos2x-sin\left(x+\dfrac{\Omega}{3}\right)=0\)
=>\(sin\left(x+\dfrac{\Omega}{3}\right)=cos2x=sin\left(\dfrac{\Omega}{2}-2x\right)\)
=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{3}=\dfrac{\Omega}{2}-2x+k2\Omega\\x+\dfrac{\Omega}{3}=\Omega-\dfrac{\Omega}{2}+2x+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}3x=\dfrac{\Omega}{6}+k2\Omega\\-x=\dfrac{1}{6}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Omega}{18}+\dfrac{k2\Omega}{3}\\x=-\dfrac{1}{6}\Omega-k2\Omega\end{matrix}\right.\)

Ta có : sin2 x + cos2 x = 1 ⇒ sin2 x = 1 – cos2 x.
⇒ P = 3.sin2 x + cos2 x
= 3.(1 – cos2x) + cos2 x
= 3 – 3.cos2x + cos2x
= 3 – 2.cos2x
= 3 – 2.(1/3)2
= 3 – 2/9
= 25/9.
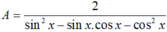

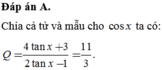
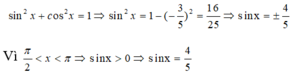

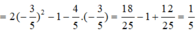
cos2x + sin2x=1
=>sin2x=1-cos2x=0.75
=>sinx=\(\pm\)\(\sqrt{3}\)/2
A= \(\dfrac{0,5+2.0,75}{0,5^2\pm\dfrac{\sqrt{3}}{2}}\)= \(\dfrac{-8\pm16\sqrt{3}}{11}\)