Trong mặt phẳng tọa độ cho điểm M(-10;1) và điểm M’(3;8). Phép tịnh tiến theo vecto biến M thành M’, thì tọa độ vecto là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
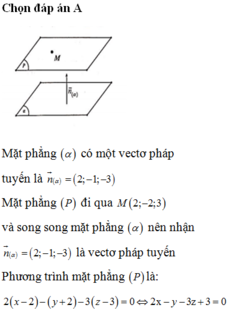
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.

Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
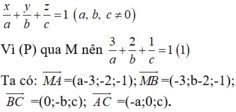
Vì M là trực tâm của tam giác ABC nên:
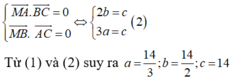
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.

N đối xứng M qua P \(\Leftrightarrow\) P là trung điểm MN
\(\Rightarrow\left\{{}\begin{matrix}x_N=2x_P-x_M=18\\y_N=2y_P-y_M=-10\end{matrix}\right.\) \(\Rightarrow N\left(18;-10\right)\)

Ta có: x'- x = 13; y'- y = 7
Đáp án C