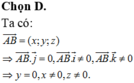cho mặt phẳng tọa độ xOy có điểm A(3;2) và điểm B(7;6). tìm tọa độ gia điểm của đường trung trực AB với đường thẳng y=3x-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 2 2021
b) Phương trình hoành độ giao điểm là:
\(-2x^2=x-3\)
\(\Leftrightarrow-2x^2-x+3=0\)
\(\Leftrightarrow-2x^2+2x-3x+3=0\)
\(\Leftrightarrow-2x\left(x-1\right)-3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(-2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\-2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\-2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số y=x-3, ta được:
y=1-3=-2
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=x-3, ta được:
\(x=-\dfrac{3}{2}-3=-\dfrac{9}{2}\)
Vậy: M(1;-2) và \(N\left(-\dfrac{3}{2};-\dfrac{9}{2}\right)\)
CM
7 tháng 10 2018
Chọn B.
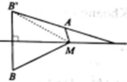
Dễ thấy A, B nằm khác phía so với mặt phẳng (xOy). Gọi B’ là điểm đối xừng với B qua (xOy). Thế thì B ' - 1 ; 4 ; 3 và M B = M B ' . Khi đó
Đẳng thức xảy ra khi và chỉ khi M, A, B’ thẳng hàng và M nằm ngoài đoạn AB’. Như vậy M cần tìm là giao điểm của đường thẳng AB’ và mặt phẳng (xOy). Đường thẳng AB có phương trình
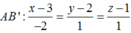
Từ đó tìm được M(5, 1, 0).
CV
0
6 tháng 4 2020
\(\overrightarrow{AB}=\left(-3;-3\right)=>AB:x+y-2=0=>y=x+2\)
Thay x = 2; y = 4 vào pt đường thẳng AB ta được 4 = 2 + 2 (luôn đúng )
=> điểm C thuộc đường thẳng AB , tương tự điểm B cũng thuộc đường thẳng AB
Vậy suy ra 3 điểm A,B,C thẳng hàng
CM
24 tháng 10 2017
Đáp án D
Phương pháp giải:
Xác định tọa độ hình chiếu trên mặt phẳng và lấy trung điểm ra tọa độ điểm đối xứng
Lời giải:
Hình chiếu của A(2;1;-3) trên mặt phẳng (Oyz) là H(0;1;-3)
Mà H là trung điểm của AA' suy ra tọa độ điểm A'(-2;1;-3)