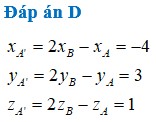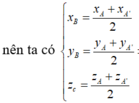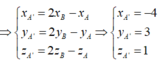Trong không gian tọa độ Oxyz cho sáu điểm A(2;0;0), A’(6;0;0), B(0;3;0), B’(0;4;0), C(0;0;3), C’(0;0;4). Tính côsin của góc giữa hai mặt phẳng mp(ABC) và mp(A'B'C').
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Vì G′ là trọng tâm của tam giác A′B′C′ nên ta có:
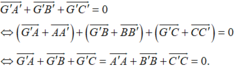
Do đó G′ cũng là trọng tâm của tam giác ABC. Vậy 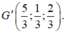

Đáp án B
Vì G′ là trọng tâm của tam giác A′B′C′ nên ta có:
![]()
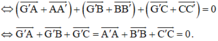
Do đó G′ cũng là trọng tâm của tam giác ABC.

Ta có ![]()
![]()
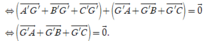
Suy ra G' cũng là trọng tâm của tam giác ABC nên có tọa độ ![]()
Chọn C.

Đáp án C.
Gọi điểm H là hình chiếu của A 4 ; 1 ; − 2 trên mặt phẳng O x z , khi đó H 4 ; 0 ; − 2 .
Điểm A' đối xứng với A 4 ; 1 ; − 2 qua mặt phẳng O x z nên H 4 ; 0 ; − 2 là trung điểm AA' . Khi đó A ' 2 x H − x A ; 2 y H − y A ; 2 z H − z A → A ' 4 ; − 1 ; − 2

Đáp án A
Dễ thấy tọa độ trung điểm của đoạn thẳng AB là điểm.