viết phương trình đường thẳng trong mỗi trường hợp sau
a) đường thẳng có hệ So goc la -3 va di qua diem A(-2;3)
b) đường thẳng cắt trục tung tại điểm có tung độ=2 và song song với đường thẳng y=1/3x-+1
c) đường thẳng cắt trục hoành tại điểm có hoành độ =3 va song song với đường thẳng y=2x+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 10 2022
a: Vì hệ số góc là -3 nên a=-3
=>y=-3x+b
Thay x=-2 và y=3 vào (d),ta được:
b+6=3
=>b=-3
b: Vì (d)//y=1/3x+1 nên a=1/3
=>y=1/3x+b
Thay x=0 và y=2 vào (d), ta được:
1/3*0+b=2
=>b=2
c: Vì (d)//y=2x+1 nên a=2
=>y=2x+b
Thay x=3 và y=0 vào (d), ta được:
b+6=0
=>b=-6
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
d nhận (1;-2) là 1 vtcp
a. d' song song d nên nhận (1;-2) là 1 vtcp
Phương trình d': \(\dfrac{x+5}{1}=\dfrac{y-2}{-2}\)
b. d' vuông góc d nên nhận \(\left(2;1\right)\) là 1 vtcp
Phương trình d': \(\dfrac{x+5}{2}=\dfrac{y-2}{1}\)
CM
28 tháng 1 2019
Vecto chỉ phương của đường thẳng d là a = (2;3;4) (vì d// ∆ )
Vậy pt tham số của đường thẳng d là: x = 2 + 2 t y = - 3 t z = - 3 + 4 t
CM
5 tháng 6 2018
a) Phương trình đường thẳng Δ đi qua M(–5; –8) và có hệ số góc k = –3 là:
y = –3.(x + 5) – 8 ⇔ 3x + y + 23 = 0.
b) Ta có: A(2; 1), B(–4; 5) ⇒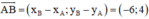 
Δ đi qua hai điểm A(2; 1) và B(–4; 5)
⇒ Δ nhận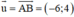 
là một vtcp
⇒ Δ nhận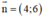 
là một vtpt.
Phương trình tổng quát của đường thẳng Δ là:
(Δ) : 4(x – 2) + 6(y -1) = 0
Hay 4x + 6y – 14 = 0 ⇔ 2x + 3y – 7 = 0.
CM
2 tháng 9 2018
Phương trình tham số của đường thẳng Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương
a
→
= (3; 3; 1) là: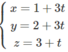 
Phương trình chính tắc của ∆ là:
31 tháng 1 2022
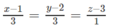
a: Vì (d)//y=-2x+1 nên a=-2
Vậy: (d): y=-2x+b
Thay x=-2 và y=3 vào (d), ta được:
b+4=3
hay b=-1
b: Vì (d) trùng với y=-x+3 nên a=-1 và b=3
c: Vì (d) cắt đường thẳng y=3x-2 nên a<>3
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2022
1. Phương trình d có dạng:
\(y=2\left(x-1\right)+1\Leftrightarrow y=2x-1\)
2. Do d tạo chiều dương trục Ox một góc 30 độ nên d có hệ số góc \(k=tan30^0=\dfrac{\sqrt{3}}{3}\)
Phương trình d:
\(y=\dfrac{\sqrt{3}}{3}\left(x-1\right)+2\Leftrightarrow y=\dfrac{\sqrt{3}}{3}x+\dfrac{6-\sqrt{3}}{3}\)
3. Do d tạo với trục Ox một góc 45 độ nên có hệ số góc thỏa mãn:
\(\left|k\right|=tan45^0\Rightarrow\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y=1\left(x-3\right)+4\\y=-1\left(x-3\right)+4\end{matrix}\right.\)