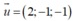Trong không gian (Oxy) cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là , phương trình đường phân giác trong góc C là . Biết rằng là một véc tơ chỉ phương của đường thẳng AB. Tính giá trị biểu thức T=m²+n².
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Ta có AB=3, AC=6. Gọi I (x; y; z) là điểm thuộc cạnh BC sao cho AI là phân giác trong của góc A

Phương trình mặt phẳng (Oxy) là: z=0.
Giao điểm của đường thẳng AI với mặt phẳng (Oxy) là M (2; 7/3; 0)
Vậy 3b-a=5.

Đáp án A
![]()
=> ∆ ABC vuông tại A
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC, I(0;2;0)
Đường thẳng d qua tâm I và vuông góc mặt phẳng (ABC) được xác định
q u a I ( 0 ; 2 ; 0 ) V T C P : u → = 1 2 A B → , A C → = ( 3 ; - 1 ; 5 )
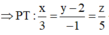
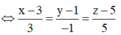
Vậy phương trình của d là x - 3 3 = y - 1 - 1 = z - 5 5

Chọn B.
Đường thẳng AB có phương trình là
![]()
Khoảng cách từ O tới đường thẳng AB bằng
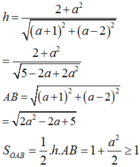
Diện tích tam giác OAB đạt giá trị nhỏ nhất bằng 1 khi a = 0

a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = - 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = - 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { - 1; - 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { - 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { - 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.





Chọn C
Gọi M là trung điểm AC.
Trung tuyến BM có phương trình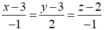 suy ra M (3-m;3+2m;2-m) => C (4 – 2m; 3 + 4m; 1 – 2m).
suy ra M (3-m;3+2m;2-m) => C (4 – 2m; 3 + 4m; 1 – 2m).
Vì C nằm trên đường phân giác trong góc C nên
Gọi A' là điểm đối xứng của A qua phân giác trong góc C, khi đó A' (2+4a;5-2a;1-2a) và A’ ∈ BC.
Véc tơ chỉ phương của đường thẳng chứa phân giác trong góc C là