Bài 1: Tính tổng tất cả T các nghiệm thuộc đoạn [0;200\(\pi\)] của phương trình 2cos2x+3sinx+3=0
Bài 2: Tìm số nghiệm của phương trình cos2x+3|cosx|-1=0 trong đoạn \(\left[\frac{-\pi}{2};\frac{\pi}{2}\right]\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BP
0
(thỏa mãn) 
CM
22 tháng 3 2019
Chọn A.
Phương trình 
Xét hàm số f(t) = 2017t + t ; ta có f’(t) = 2017tln2017 + 1 > 0 mọi x
Suy ra hàm số đồng biến trên R.
Nhận thấy (*) có dạng f( sin2x) = f(cos2x) ; do đó: sin2x = cos2x
Vì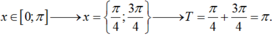 
CM
22 tháng 6 2019
Đáp án A
Ta có sin 2 2 x + 3 sin 2 x + 2 = 0 ⇔ sin 2 x + 1 sin 2 x + 2 = 0 ⇔ sin 2 x = - 1 ⇔ 2 x = - π 2 + k 2 π ⇔ x = - π 4 + k π mà x ∈ 0 ; 10 π suy ra 0 ≤ - π 4 + k π ≤ 10 π ⇔ 1 4 ≤ k ≤ 41 4 → k ∈ ℤ k = 1 ; 2 ; . . . ; 10
Vậy tổng tất cả các nghiệm của phương trình là T = 10 . - π 4 + 1 + 2 + . . . + 10 π = 105 2 π .
CM
6 tháng 3 2019
Đáp án B
Điều kiện tan x > 0
PT ⇔ e 2 2 sin x - cos x = sin x cos x ⇔ sin x e 2 2 sin x = cos x e 2 2 cos x
Xét hàm số y = f t = t e 2 2 t t - 1 ; 1
Khi đó f ' t = e 2 2 t 1 - t 2 2 e 2 t > 0 ∀ t - 1 ; 1 do đó hàm số f(t) đồng biến trên [-1;1]
Ta có f sin x = f cos x ⇔ cos x ⇔ tan x = 1 ⇔ x = π 4 + k π
Với x ∈ 0 ; 50 π ⇒ k = 0 ; 1 ; 2 ; . . . ; 49 ⇒ tổng nghiệm của pt là
50 π 4 + 1 + 2 + . . . + 49 π = 2475 2 π
\(2\left(1-sin^2x\right)+3sinx+3=0\)
\(\Leftrightarrow-2sin^2x+3sinx+5=0\Rightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\frac{5}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=-\frac{\pi}{2}+k2\pi\)
\(0\le-\frac{\pi}{2}+k2\pi\le200\pi\Rightarrow1\le k\le100\) (có 100 nghiệm)
Tổng các nghiệm:
\(\sum x=-\frac{\pi}{2}.100+\sum\limits^{100}_{k=1}2k\pi=10050\pi\)
2.
\(\Leftrightarrow2cos^2x-1+3\left|cosx\right|-1=0\)
\(\Leftrightarrow2\left|cosx\right|^2+3\left|cosx\right|-2=0\Rightarrow\left[{}\begin{matrix}\left|cosx\right|=\frac{1}{2}\\\left|cosx\right|=-2\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\cosx=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\pm\frac{\pi}{3}+k2\pi\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Pt có 2 nghiệm trên đoạn đã cho \(x=\pm\frac{\pi}{3}\)