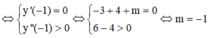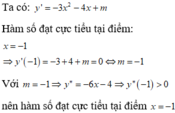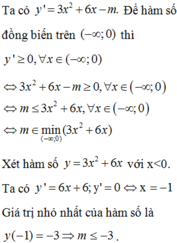y = | x3 + 2x2 -mx + m-1 |. Xđ m để max trên [0;2] = 20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có f ' x < 0 ∀ x ∈ 0 ; 2 ⇔ 3 x 2 - 4 x - m < 0 ⇔ m > 3 x 2 - 4 x
Xét hàm số g x = 3 x 2 - 4 x trên khoảng ( 0;2 )
Lập bảng biến thiên, ta suy ra m ≥ 4
Đáp án D

Ta có y ' = 3 x 2 - 4 x + m
Hàm số đạt cực trị tại x = 1 thì y'(1) = 0 ⇒ 3 . 1 2 - 4 . 1 + m = 0 ⇒ m = 1
Với m = 1 thì hàm số đã cho trở thành y = x 3 - 2 x 2 + x + 1
Ta có y ' = 3 x 2 - 4 x + 1 , y'' = 6x - 4 Vì y''(1) = 2 > 0 nên hàm số đạt cực tiểu tại x = 1.
Do vậy không có m thỏa mãn. Chọn đáp án D.
Chú ý. Sai lầm có thể gặp phải: khi giải y'(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.

Đáp án A.
Ta có: y’ = -3x2 + 4x + m.
y’’ = -6x + 4.
+ y’(1) = 0 <=> -3 + 4 + m = 0 ó m = -1.
+ y’’(1) = -2 < 0 thỏa

Đáp án C
Phương pháp:
Hàm số bậc ba y = f(x) đạt cực tiểu tại x = x0 khi và chỉ khi
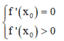
Cách giải:
![]()
![]()
![]()
![]()