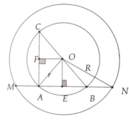
Bài tập 1:Cho đường tròn đồng tâm O, bán kính lần lượt R=5cm,r=2cm.lấy 2 điểm A,B thuộc (O;2) sao cho góc AOB=70 độ.Tia OA,OB cắt đường tròn (O;R) tại D và E, lấy điểm C thuộc đường tròn (O;r).
a) tính góc DOE, góc DCE.
b)Tính độ dài cung đường tròn (O;R) ;(O;r); độ dài cung tròn DE
c) Tính diện tích hình tròn (O;r) và hình quạt tròn DOE.(Lấy Pi=3,14).
Bài tập 2: Cho tam giác ABC nhọn,BC cố định.Kẻ đường cao AH và BK cắt nhau tại G.
a) Chứng minh tứ giác CHGK nội tiếp và tìm đường kính.
b)AH.BC=BK.AC
c)Vẽ đường tròn đường kính BC.Lấy điểm M thuộc đường tròn này.Tìm quỹ tích điểm N nằm trên tia BM sao cho MN=AC
ad và mọi người giải chi tiết và cho em hình minh họa luôn nhé ạ! Em cảm ơn nhiều ạ!