Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD có AB:x+3y-4=0. AD:x-2y+1=0 , M(2;2) là trung điểm của AB. BC : ax-2y+c=0 . Tính P= \(a^2+c^2\) .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
20 tháng 3 2021
Phương trình đường thẳng qua O và song song AB có dạng: x−y=0x−y=0
⇒⇒ Tọa độ M là nghiệm của hệ: {x+3y−6=0x−y=0{x+3y−6=0x−y=0 ⇒M(32;32)⇒M(32;32)
Phương trình đường thẳng BC qua M, nhận (1;1)(1;1) là 1 vtpt có dạng:
1(x−32)+1(y−32)=0⇔x+y−3=01(x−32)+1(y−32)=0⇔x+y−3=0
Tọa độ B là nghiệm của hệ: {x−y+5=0x+y−3=0{x−y+5=0x+y−3=0 ⇒B⇒B
M là trung điểm BC ⇒⇒ tọa độ C
O là trung điểm AC ⇒⇒ tọa độ A
O là trung điểm BD
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2020
Phương trình đường thẳng qua O và song song AB có dạng: \(x-y=0\)
\(\Rightarrow\) Tọa độ M là nghiệm của hệ: \(\left\{{}\begin{matrix}x+3y-6=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow M\left(\frac{3}{2};\frac{3}{2}\right)\)
Phương trình đường thẳng BC qua M, nhận \(\left(1;1\right)\) là 1 vtpt có dạng:
\(1\left(x-\frac{3}{2}\right)+1\left(y-\frac{3}{2}\right)=0\Leftrightarrow x+y-3=0\)
Tọa độ B là nghiệm của hệ: \(\left\{{}\begin{matrix}x-y+5=0\\x+y-3=0\end{matrix}\right.\) \(\Rightarrow B\)
M là trung điểm BC \(\Rightarrow\) tọa độ C
O là trung điểm AC \(\Rightarrow\) tọa độ A
O là trung điểm BD \(\Rightarrow\) tọa độ D
CM
19 tháng 1 2017
Gọi D(x; y)
Ta có A D → = x + 2 ; y và B C → = 4 ; − 3 .
Vì ABCD là hình bình hành nên A D → = B C →
x + 2 = 4 y = − 3 ⇔ x = 2 y = − 3 ⇒ D 2 ; − 3 .
Chọn A.
MK
20 tháng 12 2021
1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)
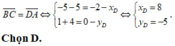
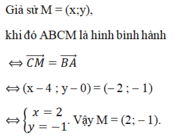
A là giao điểm AB và AD nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+3y-4=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow A\left(1;1\right)\)
\(M\left(2;2\right)\) là trung điểm AB \(\Rightarrow B\left(3;3\right)\)
\(BC//AD\Rightarrow\frac{a}{1}=\frac{-2}{-2}\Rightarrow a=1\)
Pt BC: \(x-2y+c=0\)
DO BC qua B nên: \(3-2.3+c=0\Rightarrow c=3\)
\(\Rightarrow a^2+c^2=10\)