32. Cho hai điểm A (2;1;-1); B(0;3;1). Biết tập hợp các điểm M ∈ mp (P): x+y+z+3=0 thỏa mãn 2.MA2 - MB2 = 4 là đường tròn có bán kính r. Tính r.
Giúp e với mn ơi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
![]()
![]()
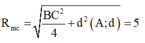
vậy phương trình mặt cầu cần tìm là
x 2 + y 2 + z + 2 2 = 25

Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).

Chọn A
Ta có trung điểm của đoạn thẳng AB là điểm I(0;1;-1). Đường thẳng d có vecto chỉ phương là u=(1;-1;2). Vậy phưng trình đường thẳng đi qua trung điểm của đoạn thẳng
AB và song song với d là:
![]()

Đáp án A
Phương pháp giải:
Vì điểm M thuộc d nên tham số hóa tọa độ điểm M, tính tổng M A 2 + M B 2 đưa về khảo sát hàm số để tìm giá trị nhỏ nhất
Lời giải:
Vì ![]() suy ra
A
M
→
=
(
t
-
2
;
4
-
2
t
;
2
t
)
B
M
→
=
(
t
;
2
-
2
t
;
2
t
-
2
)
suy ra
A
M
→
=
(
t
-
2
;
4
-
2
t
;
2
t
)
B
M
→
=
(
t
;
2
-
2
t
;
2
t
-
2
)
Khi đó ![]()
![]()
Dễ thấy ![]()
![]()
Vậy Tmin = 10. Dấu bằng xảy ra khi và chỉ khi t = 1 => M(2;0;5)

Đáp án A
Phương pháp giải:
Vì điểm M thuộc d nên tham số hóa tọa độ điểm M, tính tổng M A 2 + M B 2 đưa về khảo sát hàm số để tìm giá trị nhỏ nhất
Lời giải:
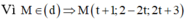
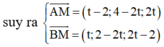
Khi đó T = M A 2 + M B 2
![]()
![]()
Dễ thấy
![]()
![]()
![]()
Dấu bằng xảy ra khi và chỉ khi t =1 => M(2;0;5)
Gọi \(N\left(4;-1;-3\right)\Rightarrow2\overrightarrow{NA}-\overrightarrow{NB}=0\)
\(2MA^2-MB^2=4\)
\(\Leftrightarrow2\left(\overrightarrow{MN}+\overrightarrow{NA}\right)^2-\left(\overrightarrow{MN}+\overrightarrow{NB}\right)^2=4\)
\(\Leftrightarrow MN^2+2NA^2-NB^2+2\overrightarrow{MN}\left(2\overrightarrow{NA}-\overrightarrow{NB}\right)=4\)
\(\Leftrightarrow MN^2=4+NB^2-2NA^2=28\)
\(\Rightarrow MN=2\sqrt{7}\Rightarrow\) M thuộc mặt cầu (C) tâm N bán kính \(R=2\sqrt{7}\) có pt:
\(\left(x-4\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=28\)
Mà \(M\in\left(P\right)\Rightarrow\) quỹ tích M là đường tròn giao tuyến của mặt phẳng (P) và mặt cầu (C)
Theo định lý Pitago: \(r=\sqrt{R^2-d^2}\) với \(d\) là khoảng cách từ N tới mặt phẳng (P)
Bạn tự tính và thay số nốt đoạn còn lại.