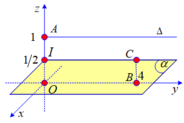
Trong không gian với hệ trục tọa độ Oxyz, xét các điểm A(0;0;1), B(m;0;0) C(0;n;0) và D(1;1;1) với m>0,n>0 và m+n=1. Biết rằng khi m,n thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng (ABC) và đi qua D. Tính bán kính R của mặt cầu đó?
A.R=1
B.R=\(\dfrac{\sqrt{2}}{2}\)
C.R=\(\dfrac{3}{2}\)
D.R=\(\dfrac{\sqrt{3}}{2}\)



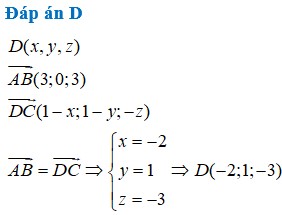
Chọn C