Cho hình chữ nhật ABCD có D(-3;1), B thuộc d: x-2y-5=0. E là giao của đường tròn tâm C bán kính CA với đt AB. Hình chiếu vuông góc của A lên CE là N(6;-2). Tìm A,B,C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1
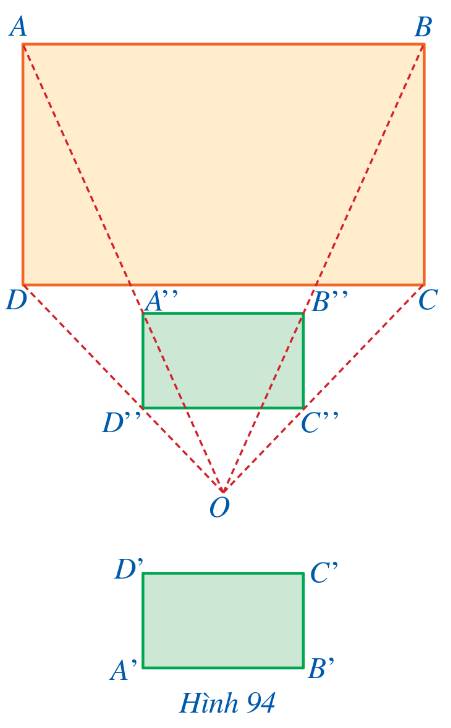
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau
CM
27 tháng 9 2018
Hướng dẫn giải:
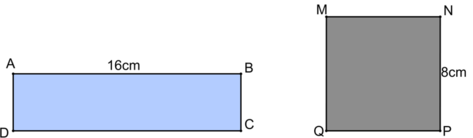
Khoanh vào D. 40cm.
Giải thích:
Diện tích hình vuông (hình chữ nhật) là:
8 x 8 = 64 ( c m 2 )
Chiều rộng hình chữ nhật là:
64 : 16 = 4 (cm)
Chu vi hình chữ nhật là:
(16 + 4) x 2 = 40 (cm)
10 tháng 1 2023
a. Ta có mỗi hình tam giác có được từ đề bài là: tam giác AED, tam giác EDC và tam giác ECB, tam giác ADC và tam giác BDC.
Diện tích tam giác AED là:
\(\dfrac{1}{2}.AD.AE=\dfrac{1}{2}.4.2=4\) cm vuông
Diện tích tam giác EBC là:
\(\dfrac{1}{2}.4.3=6\) cm vuông
Với tam giác EDC ta kẻ đường cao EH xuống DC
=> EH = BC = 4 cm
DC = AB = 2 + 3 = 5 cm
Diện tích tam giác EDC là:
\(\dfrac{1}{2}.4.5=10\) cm vuông
Diện tích tam giác ADC là:
\(\dfrac{1}{2}.AD.DC=\dfrac{1}{2}.4.5=10\) cm vuông
Diện tích tam giác ABC là:
\(\dfrac{1}{2}.BC.DC=\dfrac{1}{2}.4.5=10\) cm vuông
b. Diện tích hcn ABCD là: 4 x 5 = 20 cm vuông
Mà diện tích tam giác EDC là: 10 cm vuông
=> Tỉ số diện tích của hình tam giác EDC và diện tích hcn ABCD là:
\(\dfrac{10}{20}=\dfrac{1}{2}\)
và 
. 
và 
.