Cho hình bình hành ABCD có DT = 4 biết A(1;0) và B(2;0). Giao điểm I của 2 đg chéo AC và BD nằm trên đg thẳng y=x. Tìm tọa độ C&D.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình bình hành ABCD là hình chữ nhật( vì có 1 góc vuông)
Diện tích hình chữ nhật ABCD là
S= AB *AC= 3*5= 15 cm vuông

Đáp án C
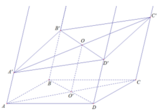
Trên Ax lấy điểm A’ sao cho AA’= x
Trên By lấy điểm B’ sao cho BB’ = y
Trên Cz lấy điểm C’ sao cho CC’ = z
Gọi α là mặt phẳng chứa tia Cz và Dt
Xét (A’B’C’) và α có:
C’ là điểm chung
A’B’ // α
⇒ giao tuyến của α và (A’B’D’) là đường thẳng d đi qua C’ và song song với A’B’
Trong mặt phẳng α , ta có: d cắt Dt tại D’
Gọi O = A C ∩ B D , O ' = A C ' ∩ B ' D '
Xét hình thang AA’C’C có: OO’ là đường trung bình
⇒ O O ' = A A ' + C C ' 2 = x + z 2
Xét tam giác BDD’D có: OO’ là đường trung bình
⇒ O O ' = D D ' + B B ' 2 ⇒ DD’ = x + z – y
Dễ thấy pt (AB): y=0 : trục hoành
Gọi H là chân đường vuông góc kẻ từ I đến AB, đặt IH=a
=> I(a;a) ( do (AB) là trục hoành và I thuộc đường thẳng x=y)
*Sử dụng công thức diện tích hình bình hành=> tính được IH => tọa độI ( hai trường hợp)
Vì I là trung điểm AC, BD => tọa độ C,D