Tìm \(a\) và \(b\) :
a) Để đường thẳng \(y=ax+b\) đi qua hai điểm \(A\left(-5;3\right),B\left(\dfrac{3}{2};-1\right)\).
b) Để đường thẳng \(ax-8y=b\) đi qua điểm \(M\left(9;-6\right)\) và đi qua giao điểm của hai đường thẳng \(\left(d_1\right):2x+5y=17,\left(d_2\right):4x-10y=14\).

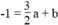
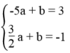
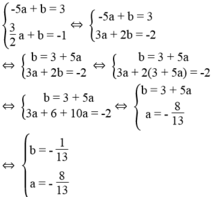
a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-5a+b=3\\\dfrac{3}{2}a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{8}{13}\\b=-\dfrac{1}{13}\end{matrix}\right.\)
b: Tọa độ giao điểm của (d1) và (d2) là;
\(\left\{{}\begin{matrix}2x+5y=17\\4x-10y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\)
Vì (d3) đi qua M(9;-6) và N(6;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}6a-8=b\\9a+48=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a-b=8\\9a-b=-48\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{56}{3}\\b=-120\end{matrix}\right.\)