Xét ba số x ; y ; z tm :
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\) và \(\left|x-y\right|\) \(=\dfrac{z^2}{12}\) . Tìm giá trị lớn nhất của biểu thức yz-x?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.
Cách giải: Ta có 
BBT:
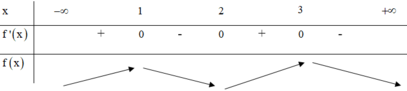
Từ BBT ta thấy (I) đúng, (II) sai.
Với ![]() => Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=> Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=>(III) đúng.
Vậy có hai khẳng định đúng

Đáp án C
Ta có f ' x = 0 ⇔ x = 1 ; 2 ; 3 ⇒ hàm số có 3 điểm cực trị
Lại có g x = f x - m - 2018 ⇒ g ' x = f ' x = 0 ⇒ có 3 nghiệm phân biệt
Suy ra phương trình f x = m + 2018 có nhiều nhất 4 nghiệm
Xét y = f x + 1 ⇒ y ' = f ' x + 1 < 0 ⇔ [ x + 1 ∈ 1 ; 2 x + 1 ∈ 3 ; + ∞ ⇔ [ 0 < x < 1 x > 2
Suy ra hàm số y = f(x + 1) nghịch biến trên khoảng (0;1).

Đáp án B
Giả sử số hiệu nguyên tử của X, Y lần lượt là ZX, ZY
Ta có hpt 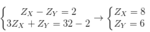
ZZ = 17 - ZX - ZY = 17 - 8 - 6 = 3.
Cấu hình electron của X, Y, Z là
8X: 1s22s22s4 → X thuộc chu kì 2, nhóm VIA.
6Y: 1s22s22p2 → Y thuộc chu kì 2, nhóm IVA.
3Z: 1s22s1 → Z thuộc chu kì 2, nhóm IA.
→ Chọn B.

Tổng của 2 số đầu là:
13 x 3 = 26
Tổng của 3 số là:
11 x 3 = 33
Số thứ 3 là:
33 - 26 = 7
Đáp số: 7

Đáp án A
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f (x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f ( x ) = x ta có D= R nên hàm số f(x) liên tục trên R.
Nhưng ta có l i m x → 0 + f ( x ) - f ( 0 ) x - 0 = l i m x → 0 + x - 0 x - 0 = l i m x → 0 + x - 0 x - 0 = 1 l i m x → 0 - f ( x ) - f ( 0 ) x - 0 = l i m x → 0 - x - 0 x - 0 = l i m x → 0 - - x - 0 x - 0 = - 1
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.

+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
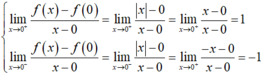
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Lời giải:
Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t\Rightarrow \left\{\begin{matrix} x=2t\\ y=3t\\ z=4t\end{matrix}\right.\)
Ta có: \(|x-y|=\frac{z^2}{12}\Leftrightarrow |2t-3t|=\frac{16t^2}{12}\)
\(\Leftrightarrow 3|-t|=4t^2\)
Nếu \(t\geq 0\Rightarrow 4t^2=3|-t|=3t\)
\(\Leftrightarrow t(4t-3)=0\Leftrightarrow \left[\begin{matrix} t=0\\ t=\frac{3}{4}\end{matrix}\right.\)
+) \(t=0\rightarrow x=y=z=0\rightarrow yz-x=0\)
+) \(t=\frac{3}{4}\Rightarrow x=\frac{3}{2}; y=\frac{9}{4}; z=3\) \(\rightarrow yz-x=\frac{21}{4}\)
Nếu \(t<0\Rightarrow 4t^2=3|-t|=-3t\)
\(\Leftrightarrow t(4t+3)=0\Leftrightarrow t=-\frac{3}{4}\)
\(\Rightarrow x=\frac{-3}{2}; y=\frac{-9}{4}; z=-3\rightarrow yz-x=\frac{33}{4}\)
Từ các TH trên suy ra \((yz-x)_{\max}=\frac{33}{4}\)\
\(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\\\left|x-y\right|=\dfrac{z^2}{12}\end{matrix}\right.\) sử dụng t/c dãy tỷ bằng nhau
\(z=0\Rightarrow x=y=0=>yz-x=0\)
\(z\ne0\Rightarrow\dfrac{yz-x}{3z-2}=\dfrac{z}{4}\Rightarrow yz-x=\dfrac{z}{4}\left(3z-2\right)=\dfrac{3z^2-2z}{4}\) (1)
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x-y}{-1}=\dfrac{z}{4}\Rightarrow\left|x-y\right|=\dfrac{\left|z\right|}{4}=\dfrac{z^2}{12}\)\(\Rightarrow\left[{}\begin{matrix}z=0\\z=\pm3\end{matrix}\right.\)(2)
(1) và (2) =>\(Max\left(yz-x\right)=\dfrac{3.\left(-3\right)^2-2\left(-3\right)}{4}=\dfrac{33}{4}\)