Trong số đồ thị của các hàm số
y = 1 x ; y = x 2 + 1 ; y = x 2 + 3 x + 7 x − 1 ; y = x x 2 − 1 có tất cả bao nhiêu đồ thị có tiệm cận ngang?
A. 1
B. 3
C. 2
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn: C
Đồ thị hàm số (A) là đồ thị của hàm số y = x x - 1
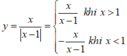
Ta giữ nguyên phần đồ thị (C) nằm phía bên phải đường thẳng x = 1 ;
lấy đối xứng phần đồ thị (C) nằm bên trái đường thẳng x = 1 qua trục hoành.
Ta được đồ thị hàm số (C).

Ta có y = x x - 1 = x x - 1 k h i x > 1 - x x - 1 k h i x < 1
Do đó đồ thị hàm số y = x x - 1 được suy từ đồ thị hàm số y = x x - 1 bằng cách:
● Giữ nguyên phần đồ thị hàm số phía bên phải đường thẳng x = 1.
● Phần đồ thị hàm số
y = x x - 1
phía bên trái đường thẳng x= 1 thì lấy đối xứng qua trục hoành.
Hợp hai phần đồ thị ở trên ta được toàn bộ đồ thị hàm số y = x x - 1
Chọn B.

Nhận xét:
Đồ thị hàm số (A) là đồ thị của hàm số y = x x - 1 C
y = x x - 1 = x x - 1 k h i x > 1 - x x - 1 k h i x < 1
Ta giữ nguyên phần đồ thị (C) nằm phía bên phải đường thẳng x=1; lấy đối xứng phần đồ thị (C) nằm bên trái đường thẳng x=1 qua trục hoành. Ta được đồ thị hàm số (C).
Chọn đáp án C.

a: Để hàm số nghịch biến thì m-2<0
hay m<2
b: Thay x=3 và y=0 vào hàm số, ta được:
\(3m-6+m+3=0\)
hay \(m=\dfrac{3}{4}\)
Đáp án C
Để hàm số có tiệm caanh ngang thì hàm số là hàm phân thức có bậc tử nhỏ hơn hoặc bằng mẫu
Vậy có hàm số y = 1 x và hàm số y = x x 2 − 1 có tiệm cận ngang