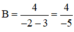Cho biểu thức với n là số nguyên. Tìm phân số B, biết n = 0; n = 10 ; n = -2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.\)
\(n-3\ne0\)
\(\Leftrightarrow n\ne3\)
\(b.\)
\(B\left(0\right)=\dfrac{-4}{3}\)
\(B\left(10\right)=\dfrac{4}{10-3}=\dfrac{4}{7}\)
\(B\left(-2\right)=\dfrac{4}{-2-3}=-\dfrac{4}{5}\)
Giải thích các bước giải:
a) Để B là phân số thì số nguyên n phải khác 0 và không thuộc Ư(4)
b)Nếu n=1 thì B=4/1-3=-2
Nếu n=2 thì B=4/2-3=-4
Nếu n=-3 thì B=4/-3-3=-2/3

a) Điều kiện: n-3 khác 0 => n khác 3
b) với n =0 => B = 4/0-3 = 4/-3
Với n =10 => B = 4/10-3 = 4/7
Với n =-2 => B = 4/-2-3 = 4/-5

\(A=\frac{3}{n+2}\)
a) \(\Leftrightarrow n+2\inƯ\left(3\right)\)
\(\Leftrightarrow n+2\in\left\{\pm1;\pm3\right\}\)
+) \(n+2=1\Leftrightarrow n=-1\)
+) \(n+2=-1\Leftrightarrow n=-3\)
+) \(n+2=3\Leftrightarrow n=1\)
+) \(n+2=-3\Leftrightarrow n=-5\)
b) \(A=\frac{3}{2};A=\frac{3}{2+2}=\frac{3}{4};A=\frac{3}{-7+2}=\frac{3}{-5}\)
\(A=\frac{3}{n+2}\)
Để A là phân số => \(n+2\ne0\)=> \(n\ne-2\)

a ) Để B là phân số thì n - 3 ≠ 0 ⇒ n ≠ 3
b ) Thay n = 0 vào biểu thức B , ta được : B = \(\frac{4}{-3}\)
Thay n = 10 vào biểu thức B , ta được : B = \(\frac{4}{10-3}=\frac{4}{7}\)
Thay n = - 2 vào biểu thức B , ta được : B = \(\frac{4}{-2-3}=\frac{4}{-5}\)

Ta có: \(A=\dfrac{3}{n+2}\left(\forall n\in Z\right)\)
a) Để \(A\) là phân số thì \(n+2\ne0\Leftrightarrow n\ne-2\)
Vậy \(n\ne-2\) thì \(A\) là phân số.
b) Thay \(n=0;n=2;n=-7\) lần lượt vào \(A\) ta có:
\(\left\{{}\begin{matrix}A=\dfrac{3}{0+2}=\dfrac{3}{2}\\A=\dfrac{3}{2+2}=\dfrac{3}{4}\\A=\dfrac{3}{-7+2}=\dfrac{-3}{5}\end{matrix}\right.\)
c) Để \(A\in Z\Rightarrow\left(n+2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow n\in\left\{-1;-3;1;-5\right\}\)
Vậy \(n\in\left\{-1;-3;1;-5\right\}\) thì \(A\in Z\)
Khi n = 0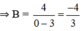
Khi n = 10 thì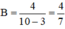
Khi n = -2 thì