Bài 7 (2) :Cho hình thang ABCD (AB//CD) ; hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với AB cắt AD lần lượt tại M và N . Chứng minh OM = ON
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Bài 7. Cho hình thang ABCD, đáy AB = 40cm, CD = 80cm, BC = 50cm, AD = 30cm. Chứng minh rằng ABCD là hình thang vuông.
S
13 tháng 9 2021
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2
=> 502= 30^2 +40^2
=> 50^2 = 2500
=> 50^2 = 50^2
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
13 tháng 9 2021
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2AG2=AD2+DG2
⇒502=302+402⇒502=302+402
⇒502=900+1600
⇒502=2500
⇒502=502
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
hơi dài nha
4 tháng 8 2021
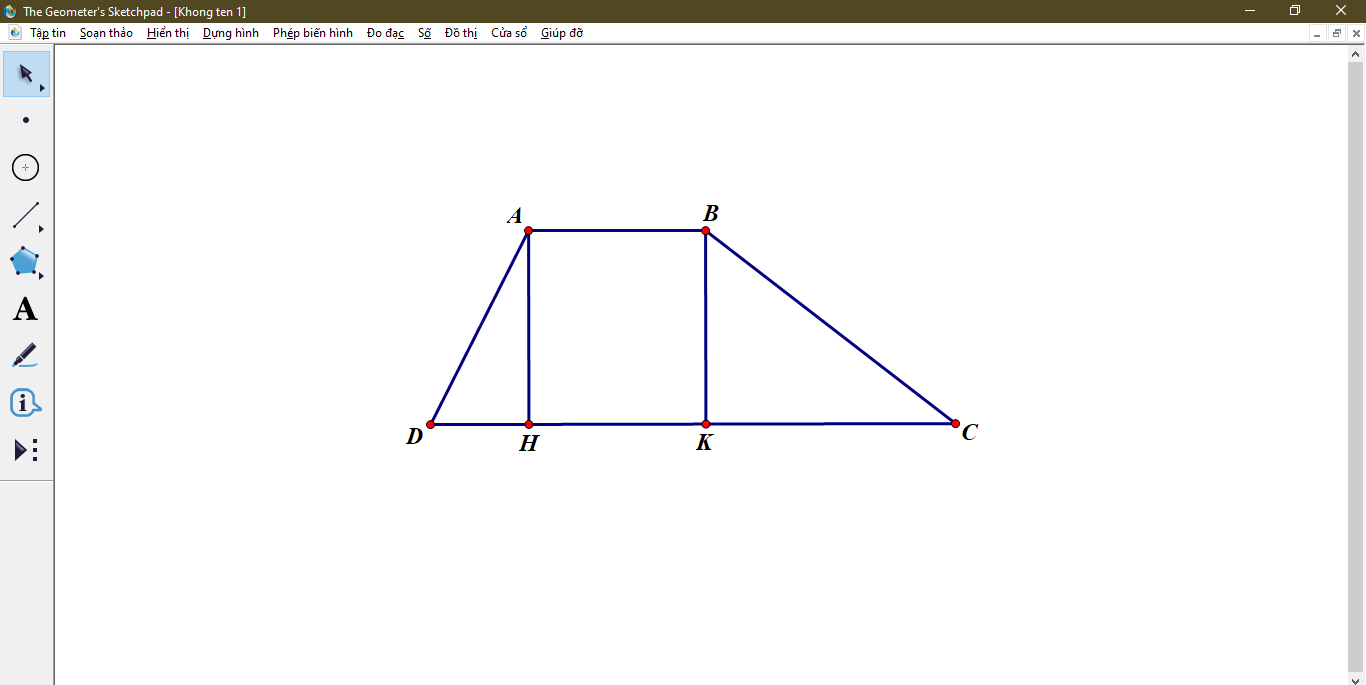
Kẻ đường cao AH và đường cao BK . ⇒AB=HK=1cm
Nên ta có : DH+CK=4 (1)
Theo tỉ số lượng giác cho tam giác ADH và BCK ta lại có :
\(\left\{{}\begin{matrix}AH=tan60\cdot DH\\BK=tan30\cdot CK\end{matrix}\right.\)\(\Rightarrow tan60\cdot DH=tan30\cdot CK\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình :
\(\left\{{}\begin{matrix}DK+CK=4\\\sqrt{3}DH-\dfrac{\sqrt{3}}{3}CK=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DH=1\\CK=3\end{matrix}\right.\)
\(\Rightarrow AH=tan60\cdot DH=\sqrt{3}\cdot1=\sqrt{3}\left(cm\right)\)
\(\Rightarrow S_{ABCD}=12\cdot AH\cdot\left(AB+CD\right)=12\cdot\sqrt{3}\cdot\left(1+5\right)=3\sqrt{3}\left(cm^2\right)\)
Tick hộ nha bạn 😘
26 tháng 8 2021
BÀI 2; Cho hình cân ABCD ( AB // CD ) ; góc A = 120 độ. Tính các góc còn lại của hình thang.
Giải:
Xét hình thang cân ABCD ta có:
góc BAD + góc ADC = 180 độ ( 2 góc trong cùng phía bù nhau do AB//CD)
=> 120 độ + góc ADC = 180 độ
=> góc ADC = 60 dộ
Vì tiws giác ABCD là hình thang cân
=> góc BAD = góc ABC = 120 độ
=> góc ADC = góc BCD = 60 độ
26 tháng 8 2021
Do AB // CD ( GT )
⇒^A+^C=180o
⇒2^C+^C=180o
⇒3^C=180o
⇒^C=60o
⇒ ^A = 60o * 2 = 120o
Do ABCD là hình thang cân
⇒ ^C = ^D
Mà ^C = 60o
⇒ ^D = 60o
AB // CD ⇒ ^D + ^B = 180o
⇒ˆB=180o − 60o = 120o
Vậy ^A = ^B = 120o ; ^C= ^D = 60o
26 tháng 8 2021
Xét 2 tam giác : Tam giác ADB và tam giác BCA có :
AB : Cạnh chung
^DAB=^CBA (Tính chất của hình thang cân)
AC = BD ( Tính chất của hình thang cân)
⇒ ΔADB = ΔBCA ( c−g−c)
⇒ ^CAB = ^DBA (2 góc tương ứng)
⇒ ^OAB = ^OBA
=> Tam giác OAB cân
=> OA = OB
=> Điều phải chứng minh
25 tháng 8 2021
Bài 6:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
25 tháng 8 2021
Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
25 tháng 8 2021
Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK và HB=KC
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{HC}\)
Do đó: KH//BC
Xét tứ gác BKHC có KH//BC
nên BKHC là hình thang
mà KC=BH
nên BKHC là hình thang cân
25 tháng 8 2021
Bài 2:
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK
Xét ΔABC có
\(\dfrac{AK}{AB}=\dfrac{AH}{AC}\)
Do đó: HK//BC
Xét tứ giác BCHK có HK//BC
nên BCHK là hình thang
mà HB=KC(ΔAHB=ΔAKC)
nên BCHK là hình thang cân
25 tháng 8 2021
Bài 3:
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{OCD}=\widehat{ODC}\)
Xét ΔODC có \(\widehat{OCD}=\widehat{ODC}\)
nên ΔODC cân tại O
Suy ra: OD=OC
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB