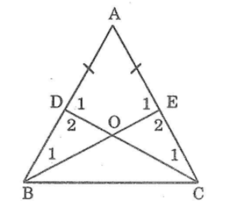
cho tam giác ABC có AB=AC. Lấy D trên cạnh AB, E trên cạnh AC: AD= AE
a; cmr: BE=CD
b; Gọi O là giao điểm của BE và CD
cmr : các tam giác BOD và tam giác COE bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{DAC}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
Suy ra: BE=CF
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC

a: XétΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó:ΔABD=ΔAED
Suy ra: BD=ED
b: ta có: BD=ED
mà ED<DC
nên BD<DC

a,
Xét Δ ADC và Δ AEB
Ta có : AD = AE (gt)
AC = AB (Δ ABC cân tại A)
\(\widehat{DAC}=\widehat{EAB}\) (góc chung)
=> Δ ADC = Δ AEB (c.g.c)
b, Ta có : Δ ADC = Δ AEB (cmt)
=> \(\widehat{ACD}=\widehat{ABE}\)
a)Xét △ABE và △ACD có
AB = AC ( △ABC cân tại A)
AD = AE (gt)
\(\widehat{A}\) là góc chung
=> △ABE = △ACD (c-g-c)
=> BE = CD ( e cạnh tương ứng)
b) Vì △ABE = △ACD
nên \(\widehat{ABE}=\widehat{ACD}\)
c)
Vì \(\widehat{ABC}=\widehat{ABE}+\stackrel\frown{EBC}\)
\(\text{}\widehat{ACB}=\widehat{ACD}+\widehat{DCB}\)
mà \(\widehat{ABE}=\widehat{ACD}\)
\(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{EBC}=\widehat{DCB}\)
=> △KBC là tam giác cân tại K

Xét ΔBEA và CDA, ta có:
BA = CA (giả thiết)
∠A chung
AE=AD (giả thiết)
Suy ra: ΔBEA = ΔCDA (c.g.c)
Vậy: BE = CD (hai cạnh tương ứng)

Hình bạn tự vẽ ạ.
a, Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(\dfrac{AD}{AB}=\dfrac{7}{14}=\dfrac{1}{2}\)
\(\dfrac{AE}{AC}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{2}\right)\)
Mà \(\widehat{A}:chung\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
b, Ta có : \(\Delta ADE\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}\)
hay \(\dfrac{7}{14}=\dfrac{ED}{18}\)
\(\Rightarrow ED=\dfrac{7.18}{14}=9\left(cm\right)\)

a)xét tg ABD và tg CBD có:
+ AB=BE(gt)
+ góc ABD = EBD (BD là phân giác)
+BD chung
=>tg ABD= tg EBD(c.gc)
b) vì tg ABD=tgEBD
=> AD=DE và góc BAD = BED (=90 độ)
=> DE ⊥ BC
=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD
c)xét tg BFE và tg BCA có:
+ Góc E = A (=90 độ)
+góc B chung
+ BE=BA
=>tg BFE =tg BCA (gcg)
=>BF=BC
=> tg BFC cân tại B
vì S là td FC
=>BS vừa là trung tuyến vừa là đường cao
=>BS⊥FC (1)
tg BFC có: D là giao của 2 đg cao CA và FE
=> D là trực tâm => BD ⊥ FC (2)
từ 1 và 2 => B,D,S thẳng hàng
Sửa đề: AB = BE (không phải AB = AE)
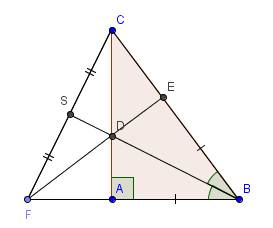
Gởi hình vẽ trước, đi công việc, tí sửa sau

A B C E D
Mình biểu diễn bằng hình vẽ trên.
Xét EAD và EDB chung đỉnh E, đáy AD gấp 2 lần đáy DB (10 : (15 -10) = 2)
=> S_EAD gấp 2 lần S_EDB => Diện tích EDB = 45 : 2 = 22,5 (cm2)
Diện tích BAE là : 45 + 22,5 = 67,5 (cm2)
Xét tam giác BAE và tam giác AEC có chung đỉnh B và đáy AE gấp 3 lần đáy EC (15 : (20-15) = 3)
=> Diện tích BAE gấp 3 lần diện tích AEC. Vậy diện tích AEC là : 67,5 : 3 =22,5 (cm2)
Vậy diện tích ABC là : 67,5 + 22,5 = 90 (cm2)