Cho hình bình hành ABCD, IK lần lượt ở trung điểm của AB, CD
a)Chứng minh AI= CK
b) Chứng minh AICK là hình bình hành
c) BD cắt AK ở CI lần lượt là MN; chứng minhDM=NM=NB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
0
Những câu hỏi liên quan
CM
17 tháng 10 2018
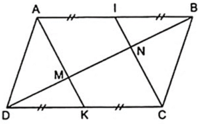
Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
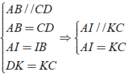
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
27 tháng 10 2020
Bài làm
a) Vì ABCD là hình bình hành
=> AB = DC (1)
Mà I là trung điểm AB => AI = IB = 1/2AB (2)
Và K là trung điểm AC => DK = KC = 1/2DC (3)
Từ (1), (2) và (3) => AI = IB = DK = KC
Vì AB // DC (vì ABCD là hình bình hành)
=> AI // KC
Xét tứ giác AICK có:
AI // KC (cmt)
AI = KC (cmt)
=> AICK là hình bình hành.
b) Xét tam giác DCF có:
KE // FC (Do AK // IC vì AICK là hình bình hành)
K là tủng điểm DC
=> KE là đường trung bình.
=> E là trung đểm DF
=> DE = EF (4)
Xét tam giác BAE có:
IF // AE (Vì AK // IF do AICK là hình bình hành)
I là trung điểm AB
=> IF là đường trung bình.
=> F là trung điểm EB
=> EF = FB (5)
Từ (4) và (5) => DE = EF = FB.
c) Vì AB // DC
=> \(\widehat{ABD}=\widehat{BDC}\)(so le trong)
Xét tam giác BIF và tam giác DKE có:
IB = DK (cmt)
\(\widehat{ABD}=\widehat{BDC}\)(cmt)
DE = FB (cmt)
=> Tam giác BIF = tam giác DKE (c.g.c)
=> IF = EK (hai cạnh tương ứng)
Xét tứ giác IFKC có:
IF = EK (cmt)
IF // EK (Do IC // AK)
=> IFKC là hình bình hành.
27 tháng 10 2020
Còn câu d và e thì xin kiếu. Vì hình rối + câu cuối mình không biết làm ^^"
CM
19 tháng 12 2017
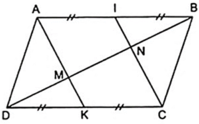
Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: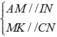
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
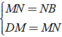⇒ DM = MN = NB
28 tháng 2 2022
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét ΔAEM có
E là trung điểm của AB
EN//AM
Do đó; N là trung điểm của BM
=>BN=NM(1)
Xét ΔDNC có
F là trung điểm của DC
FM//NC
Do đó: M là trung điểm của DN
=>DM=MN(2)
Từ (1) và (2) suy ra DM=MN=NB
c: Xét ΔADM và ΔCBN có
AD=CB
\(\widehat{ADM}=\widehat{CBN}\)
DM=BN
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
mà EN=AM/2
và MF=CN/2
nên EN=MF
Xét tứ giác MENF có
NE//MF
NE=MF
Do đó: MENF là hình bình hành
GD
5 tháng 10 2019
a, ABCD là hình bình hành ⇒AB=CD , AB//CD
Ta có: AK= \(\frac{1}{2}AB\)
CI= \(\frac{1}{2}CD\)
AB= CD ( cm trên )
⇒AK=CI
Tứ giác AICK có AK=CI ( cm trên )
AK//CI (cmtrên)
⇒AICK là hình bình hành ⇒AI // CK
c , ΔABM có KN //AM ( cm trên )
AK=KB (gt)
⇒BN=MN (1)
Chứng minh tương tự với ΔDNC ta có: DM=MN (2)
Từ (1) và (2) ⇒DM=MN=BN
21 tháng 9 2021
a: Xét tứ giác DMBN có
BM//DN
BM=DN
Do đó: DMBN là hình bình hành
b: Xét ΔAKB có
M là trung điểm của AB
MH//BK
Do đó: H là trung điểm của AK
Xét ΔCHD có
N là trung điểm của CD
NK//DH
Do đó: K là trung điểm của HC
KV
8 tháng 11 2023
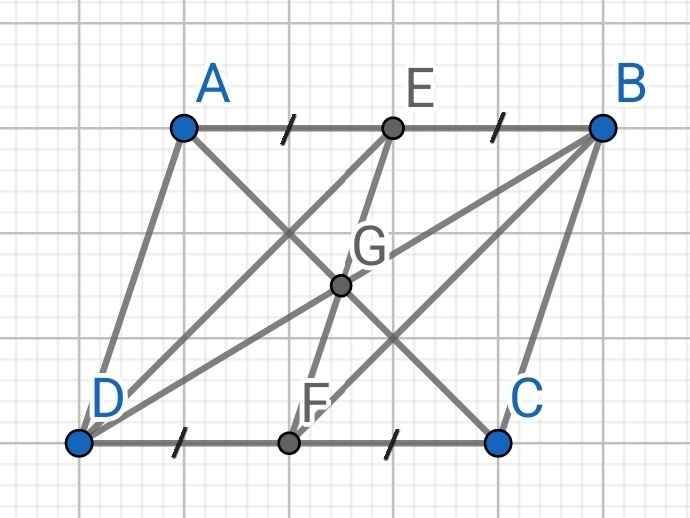a) Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ BE // DF
Do ABCD là hình bình hành
⇒ AB = CD (1)
Ta có:
E là trung điểm của AB (gt)
⇒ BE = AB : 2 (2)
F là trung điểm của CD (gt)
⇒ DF = CD : 2 (3)
Từ (1), (2) và (3) ⇒ BE = DF
Tứ giác BFDE có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BFDE là hình bình hành
b) Gọi G là trung điểm của AC
Do ABCD là hình bình hành (gt)
⇒ G là trung điểm của AC và BD (4)
Do BFDE là hình bình hành (cmt)
G là trung điểm của BD (cmt)
⇒ G là trung điểm của EF (5)
Từ (4) và (5) ⇒ AC, BD, EF cắt nhau tại G