Biết rằng đồ thị hàm số y = 4 x 2 4 x 3

PT

Pham Trong Bach

3 tháng 9 2018

Biết rằng đồ thị hàm số y = 4 x 2 + 4 x + 3 - a x + b ; a , b ∈ ℝ có đường tiệm cận ngang là đường thẳng y = 2018. Giá trị lớn nhất của P = a+b là : A. 2019 B. 2018 C. 2017 D. 2020...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

3 tháng 9 2018

Chọn đáp án A.

Đúng(0)

TN

Trúc Nguyễn

15 tháng 1 2021

cho hàm số y = -ax + 5 hãy xác định hệ số a biết rằng

a, đồ thị hàm số song song với đồ thị y = ax + b\

b, khi x = 1 + √x thì y = -4 - √3

#Hỏi cộng đồng OLM #Toán lớp 9

0

TN

Trúc Nguyễn

15 tháng 1 2021

cho hàm số y = -ax + 5 hãy xác định hệ số a biết rằng

a, đồ thị hàm số song song với đồ thị y = ax + b\

b, khi x = 1 + √x thì y = -4 - √3

#Hỏi cộng đồng OLM #Toán lớp 9

0

NH

Nguyễn Hoàng Anh

30 tháng 11 2023

biết rằng đồ thị hàm số $y=x^2-6x$ cắt đồ thị hàm số$y=-x^2-4$ tại 2 điểm $A\left(x_A;y_A\right)$ và $B\left(x_B;y_B\right)$. tính $y_A+y_B$

#Hỏi cộng đồng OLM #Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

30 tháng 11 2023

Phương trình hoành độ giao điểm là:

$x^2-6x=-x^2-4$

=>$x^2-6x+x^2+4=0$

=>$2x^2-6x+4=0$

=>$x^2-3x+2=0$

=>(x-1)(x-2)=0

=>$\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.$

Khi x=1 thì $y=-1^2-4=-1-4=-5$

Khi x=2 thì $y=-2^2-4=-8$

Vậy: A(1;-5); B(2;-8)

$y_A+y_B=\left(-5\right)+\left(-8\right)=-13$

Đúng(2)

PT

Pham Trong Bach

27 tháng 12 2017

a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị B vừa tìm được.

b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1; 3). Tìm a. Vẽ đồ thị hàm số với giá trị a tìm được

#Hỏi cộng đồng OLM #Toán lớp 9

1

CM

Cao Minh Tâm

27 tháng 12 2017

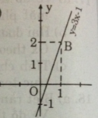
a) Thay x = 4 và y = 11 vào y = 3x + b ta được:

11 = 3.4 + b = 12 + b

=> b = 11 – 12 = -1

Ta được hàm số y = 3x – 1

- Cho x = 0 => y = -1 được A(0; -1)

- Cho x = 1 => y = 2 được B(1; 2).

Nối A, B ta được đồ thị hàm số y = 3x – 1.

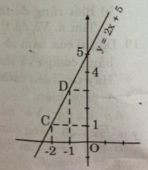
Để học tốt Toán 9 | Giải bài tập Toán 9

b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:

3 = a(-1) + 5

=> a = 5 – 3 = 2

Ta được hàm số y = 2x + 5.

- Cho x = -2 => y = 1 được C(-2; 1)

- Cho x = -1 => y = 3 được D(-1; 3)

Nối C, D ta được đồ thị hàm số y = 2x + 5.

Để học tốt Toán 9 | Giải bài tập Toán 9

Đúng(0)

Y

Yuuki

21 tháng 12 2015 - olm

a) Biết rằng điểm M(a;-2,5) thuộc đồ thị hàm số y=-2,5x². Tìm a?

b) Biết rằng điểm P(3;b) thuộc đồ thị hàm số y=|x-4|. Tìm b?

giúp mk nha m.n mk se tick cho

#Hỏi cộng đồng OLM #Toán lớp 7

0

TN

Trúc Nguyễn

14 tháng 1 2021

cho hàm số y = -ax + 5 hãy xác định hệ số a biết rằng

a, đồ thị hàm số song song với đồ thị y = ax + b

b, khi x = 1 + $\sqrt{x}$ thì y = -4 - $\sqrt{3}$

#Hỏi cộng đồng OLM #Toán lớp 9

0

HM

Hà Mi

20 tháng 8 2021

a) khảo sát và vẽ đồ thị hàm số $y=x^4-2x^2+3$

b) vẽ đồ thị hàm số $y=\left|x^4-2x^2+3\right|$

#Hỏi cộng đồng OLM #Toán lớp 12

0

NB

Nguyễn Bảo Linh

15 tháng 12 2021

1. tìm x, y biết : x/y =3/5 và 3x +y = 28

2.cho hàm số y =f(x) =ax

*khi a=2

a.vẽ đồ thị hàm số

b. tính f(-0,5);f(3/4)

*tìm hệ số a biết đò thị hàm số đi qua điểm A(-4;2)

#Hỏi cộng đồng OLM #Toán lớp 7

2

NH

Nguyễn Hoàng Minh

15 tháng 12 2021

$1,\Rightarrow\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{3x+y}{9+5}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=6\\y=10\end{matrix}\right.\\ 2,\\ a,a=2\Rightarrow y=f\left(x\right)=2x\\ b,f\left(-0,5\right)=2\left(-0,5\right)=-1\\ f\left(\dfrac{3}{4}\right)=2\cdot\dfrac{3}{4}=\dfrac{3}{2}\\ c,\text{Thay }x=-4;y=2\Rightarrow-4a=2\Rightarrow a=-\dfrac{1}{2}$

Đúng(3)

TY

Tomioka Yuko

15 tháng 12 2021

Ta có: $x/y$ = $3/5$ ⇒ $x/3$ = $y/5$

Theo tính chất của dãy tỉ số bằng nhau ta có: $x/3$ = $y/5$ = $3x/3.3$ = $y/5$ = $3x+y9/y9+5$ = $28/14$ =2

Do đó:

$x/3$ =2 ⇒x=2.3=6

$y/5$ =2 ⇒y=2.5=10

Vậy x=6 và y=10.

Đúng(1)

TM