Cho tam giác ABC : M; N lần lượt là trung điểm hai cạnh AB và AC. Nối M với N. Trên tia đối tia NM xác định điểm P sao cho NP=MN. Nối P với C.
a, CM : MP=BC.
b, CP song song AB.
c, MB = CP.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1 2022
a: Xét ΔAIB và ΔEIC có
IB=IC
\(\widehat{AIB}=\widehat{EIC}\)
IA=IE
Do đó: ΔAIB=ΔEIC
b: Xét ΔABC và ΔECB có
AB=EC
\(\widehat{ABC}=\widehat{ECB}\)
BC chung
Do đó: ΔABC=ΔECB
CM
3 tháng 11 2018
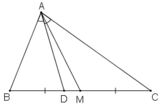
a) Ta có: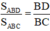 
(do hai tam giác có chung chiều cao từ đỉnh A)
ΔABC có AD là phân giác
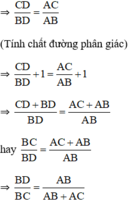
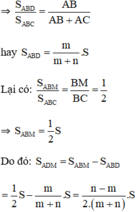
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:
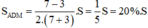
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.
2 tháng 3 2022
a: Ta có: ΔABC cân tại A
nên AB=AC
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
c: Ta có: ΔABM=ΔACN
nên AM=AN
hay ΔAMN cân tại A
LH
8 tháng 6 2021
Câu:1 Vì AM=MB , AN=NC
Nên diện tích tam giác AMN=2ABC
=> Diện tích tam gác AMN = 180:2 = 90
Bạn xem lời giải ở đây nhé:
Câu hỏi của Vy Tuyết - Toán lớp 7 - Học toán với OnlineMath