Cho đoạn thẳng MN trên hai nửa mặt phẳng đối nhau có bờ là MN vẽ các tia MX và NY trong đó MNX = x; MNY= 80-x.Tinh x để Mx song song với Ny
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D M N x y
Dpcm ANx // CNy
do AB//CD nen
=>AM // CM va MB//ND
=>AMB // CND
=>ANx // CNy
a). Ta có: góc AMx=góc B (GT)
Mà góc AMx và góc B là hai góc đồng vị.
=> Mx//BC.
Kéo dài tia Mx, cắt CD tại E.
Vì AB//CD(gt) nên AMEˆ=DEMˆ(slt)AME^=DEM^(slt)
mà theo gt AMEˆ=CNyˆAME^=CNy^ nên DEMˆ=CNyˆDEM^=CNy^
=> Mx//Ny(do có 1 cặp góc bằng nhau ở vị trí so le trong
A M x C D

A B C D M x N y
Giải:
Do AB // CD nên: \(\widehat{AMN}+\widehat{MNC}=180^o\) ( 2 góc trong cùng phía bù nhau )
\(\Rightarrow\widehat{AMx}+\widehat{xMN}+\widehat{MNC}=180^o\)
Do \(\widehat{AMx}=\widehat{CNy}\left(gt\right)\)
\(\Rightarrow\widehat{CNy}+\widehat{xMN}+\widehat{MNC}=180^o\)
\(\Rightarrow\left(\widehat{CNy}+\widehat{MNC}\right)+\widehat{xMN}=180^o\)
\(\Rightarrow\widehat{MNy}+\widehat{xMN}=180^o\)
Mà 2 góc \(\widehat{MNy},\widehat{xMN}\) ở vị trí trong cùng phía
\(\Rightarrow\)Mx // Ny ( đpcm )
Vậy...

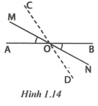
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác