Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
\(\widehat{NAC}\) chung
Do đó: ΔAMB=ΔANC
Suy ra: AM=AN
b: Xét ΔNBC vuông tại N và ΔMCB vuông tại M có
BC chung
NC=MB
Do đó: ΔNBC=ΔMCB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
=>IB=IC
Ta có: IB+IM=MB
IN+IC=NC
mà MB=NC
và IB=IC
nên IM=IN
hay ΔMIN cân tại I
c: Xét ΔNBK và ΔMCK có
NB=MC
\(\widehat{NBK}=\widehat{MCK}\)
BK=CK
Do đó: ΔNBK=ΔMCK
Suy ra: KN=KM
hayΔKMN cân tại K
a: Xét ΔABD vuông tại D và ΔACD vuông tại C có
AB=AC
AD chung
Do đó: ΔABD=ΔACD
=>DB=DC
=>D là trung điểm của BC
b: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)(ΔABD=ΔACD)
Do đó: ΔAED=ΔAFD
=>AE=AF
=>ΔAEF cân tại A
Vì tam giác ABK = tam giác ACE => AK = AE ( 2 cạnh tương ứng )
ta có \(\dfrac{AE}{AB}=\dfrac{AK}{AC}\)do AB = AC ; AE = AK ( cmt )
=> EK // BC ( Ta lét đảo )
\(\Delta\) cân tại A nên: AB = AC
mà AB = 4 \(\Rightarrow\) AC = 4
Áp dụng định lí Pytago, ta có
\(BC^2=AB^2+AC^2=4^2+4^2\\ =\sqrt{16+16}=4\sqrt{2}\)
Lời giải:
a) Xét tam giác vuông $ABH$ và $ACK$ có:
$\widehat{A}$ chung
$AB=AC$ (do $ABC$ cân tại A)
$\Rightarrow \triangle ABH=\triangle ACK$ (ch-gn)
$\Rightarrow AH=AK$
b)
Xét tam giác vuông $AKI$ và $AHI$ có:$AI$ chung
$AK=AH$ (cmt)
$\Rightarrow \triangle AKI=\triangle AHI$ (ch-cgv)
$\Rightarrow \widehat{KAI}=\widehat{HAI}$ nên $AI$ là tia phân giác $\widehat{A}$
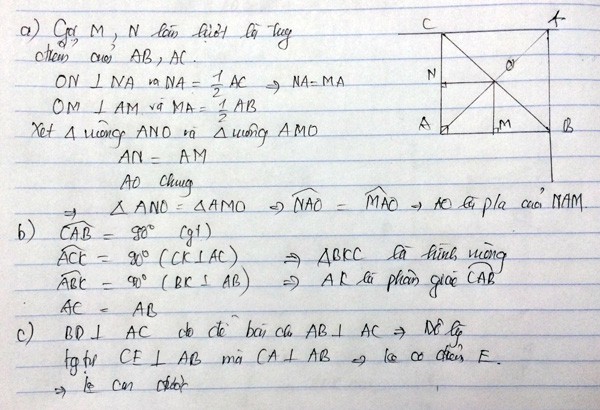
a) Xét ΔABD và ΔACE có:
∠ADB = ∠AEC = 900 (gt)
BA = AC (gt)
∠BAC (chung)
⇒ ΔABD =ΔACE (cạnh huyền – góc nhọn)
b) Có ΔABD =ΔACE ⇒ ∠ABD = ∠ACE (hai góc tương ứng)
mặt khác: ∠ABC = ∠ACB (D ABC cân tại A )
⇒ ABC – ABD =ACB – ACE ⇒ HBC = HCB
⇒ ΔBHC là tam giác cân tại H
c) Có ΔHDC vuông tại D nên HD < HC
mà HB = HC (ΔBHC cân tại H)
⇒ HD < HB
d) Gọi I là giao điểm của BN và CM
* Xét ΔBNH và ΔCMH có:
BH = CH (ΔBHC cân tại H)
∠BHN = ∠CHM (đối đỉnh)
NH = HM (gt)
ΔBNH = ΔCMH (c.g.c) ⇒ ∠HBN = ∠HCM
* Lại có: ∠HBC = ∠HCB (Chứng minh câu b)
⇒ ∠HBC + ∠HBN = ∠HCB + ∠HCM ⇒ ∠IBC = ∠ICB
⇒ IBC cân tại I ⇒ IB = IC (1)
Mặt khác ta có: AB = AC (D ABC cân tại A) (2)
HB = HC (D HBC cân tại H) (3)
* Từ (1); (2) và (3)
Þ 3 điểm I; A; H cùng nằm trên đường trung trực của BC
⇒ I; A; H thẳng hàng
⇒ các đường thẳng BN; AH; CM đồng quy