Cho hình bình hành ABCD; E, F lần lượt là trung điểm của AD, BC. Đường chéo AC cắt BE, DF lần lượt tại P, Q. Gọi R là trung điểm của đoạn thẳng BP. Chứng minh:
a) AP = PQ = QC
b) Tứ giác ARQE là hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình

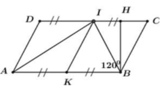
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A

Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)

A B C D A' B' C' D' M N P Q E F
Lấy E là trung điểm A'D ; F là trung điểm BC'.
Dễ dàng chứng minh được \(\Delta EQM=\Delta FNP\left(c.g.c\right)\)
Từ đó suy ra \(MQ=NP\)
CMTT có \(MN=PQ\)
Do đó \(MNPQ\)là hình bình hành.
Vậy ...
D A B C E F Q P O R
Giải
a) Trong \(\Delta\)BDC có CO và DF là trung tuyến nên giao điểm Q là trọng tâm. Do đó: OQ = \(\frac{1}{2}\)QC = \(\frac{1}{3}\)OC (1)
Tương Tự: OP = \(\frac{1}{2}\)AP = \(\frac{1}{3}\)OA (2)
Từ (1) và (2) suy ra AP = PQ = QC
b) Theo trên ta có, P là trọng tâm của \(\Delta\)ABD nên:
EP = \(\frac{1}{2}\)PB = PR (gt)
Tứ giác ARQE có: PA = PQ (cmt) ; PE = PR (cmt)
Tức là tứ giác ARQE có các đường chéo cắt nhau ở trung điểm của mỗi đường. Vậy tứ giác ARQE là hình bình hành