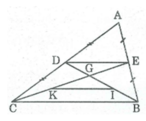
1) Cho tam giác ABC, các đường trung tuyến của BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC . CMR: DE// IK ; DE=IK
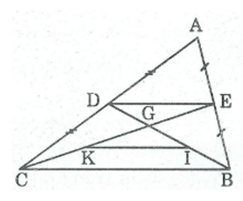
2)Cho tam giác ABC, các đường trung tuyến của BD, CE. Gọi M, N theo thứ tự là trung điểm của BE , CD . Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. CMR: MI=IK=KN


1) Bài 38 Sách bài tập - trang 84 - Toán lớp 8 | Học trực tuyến
2) Bài 40 Sách bài tập - trang 84 - Toán lớp 8 | Học trực tuyến.
1,Trong tam giác ABC ta có:
E là trung điểm của AB (gt)
D là trung điểm của AC (gt)
Nên ED là đường trung bình của tam giác ABC
⇒ED // BC và \(ED=\dfrac{BC}{2}\) (tính chất đường trung bình của tam giác) \(^{\left(1\right)}\)
Trong tam giác GBC ta có:
I là trung điểm của BG (gt)
K là trung điểm của CG (gt)
Nên IK là đường trung bình của ∆ GBC
⇒ IK // BC và \(IK=\dfrac{BC}{2}\) (tính chất đường trung bình của tam giác) \(^{\left(2\right)}\)
Từ (1) và (2) suy ra: IK // DE và IK = DE.
2,Trong tam giác ABC ta có:
-E là trung điểm của cạnh AB
-D là trung điểm của cạnh AC
Nên ED là đường trung bình của ∆ ABC
\(\Rightarrow ED//BC\) và \(ED=\dfrac{1}{2}BC\) (tính chất đường trung bình của tam giác)
Trong hình thang BCDE, ta có: BC // DE
-M là trung điểm cạnh bên BE
-N là trung điểm cạnh bên CD
Nên MN là đường trung bình hình thang BCDE ⇒ MN // DE
\(MN=\dfrac{DE+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3BC}{4}\) (tính chất đường trung bình hình thang)
Trong tam giác BED ta có:
M là trung điểm của BE
MI // DE
Suy ra: MI là đường trung bình của ∆ BED
\(\Rightarrow MI=\dfrac{1}{2}DE=\dfrac{1}{4}BC\) (tính chất đường trung bình tam giác)
Trong tam giác CED ta có:
N là trung điểm của CD
NK // DE
Suy ra: NK là đường trung bình của ∆ BED
\(\Rightarrow NK=\dfrac{1}{2}DE=\dfrac{1}{4}BC\) (tính chất đường trung bình tam giác)
\(IK=MN-\left(MI+NK\right)\)
\(=\dfrac{3}{4}BC-\left(\dfrac{1}{4}BC+\dfrac{1}{4}BC\right)=\dfrac{1}{4}BC\)
\(\Rightarrow MI=IK=KN=\dfrac{1}{4}BC\)