Cho hình thang vuông ABCD , AD= 6cm ; DC = 12cm ; AB = 2/3 DC.
a) Tính diện tích hình thang ABCD.
b) Kéo dài cạnh bên AD và CB, chúng gặp nhau tại M . Tính độ dài cạnh AM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 11 2019
Ta có: AD = AE + DE
Suy ra: DE = AD – AE = 17 – 8 = 9cm
Xét △ ABE và △ DEC, ta có:
∠ A = ∠ D = 90 0 (1)
Mà :
Suy ra: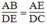 
(2)
Từ (1) và (2) suy ra : △ ABE đồng dạng △ DEC (c.g.c)
Suy ra: ∠ ABE = ∠ DEC
Trong △ ABE ta có: ∠ A = 90 0 ⇒ ∠ (AEB) + ∠ (ABE) = 90 0
Suy ra: ∠ (AEB) + ∠ (DEC) = 90 0
Lại có: ∠ (AEB) + ∠ (BEC) + ∠ (DEC) = 180 0 (kề bù)
Vậy : ∠ (BEC) = 180 0 - ( ∠ (AEB) + ∠ (DEC)) = 180 0 - 90 0 = 90 0
14 tháng 6 2023
a: AB=2/3*12=8cm
S=1/2(12+8)*6=60cm2
b: Xét ΔKDC có AB//DC
nên AB/DC=KA/KD
=>KA/(KA+6)=2/3
=>2KA+12=3KA
=>-KA=-12
=>KA=12cm
20 tháng 9 2015
đáy bé BC là
12x2/3=8(cm)
diện tích hình thang ABCD là
\(\frac{\left(8+12\right)6}{2}\)=60(cm2)
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
Tích nha các bạn