So sánh A=2002^2; B=2001*2003
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Có : A = 2002^2 = 2002.2002 = (2001+1).(2002 = 2001.2002+2002 = (2001.2002+2001)+1 = 2001.(2002+1)+1 = 2001.2003+1>2001.2003
=> A > B
k mk nha


Ta có:
\(\frac{2000}{2001}\)> \(\frac{2000}{2001+2002}\)(1)
\(\frac{2001}{2002}\)> \(\frac{2001}{2001+2002}\)(2)
Cộng các bất đẳng thức (1) và ( 2) vế với nhau:
Vậy \(\frac{2000}{2001}\)+ \(\frac{2001}{2002}\)> \(\frac{2000+2001}{2001+2002}\)hay A > B.

Giải
Ta có\(A=\frac{2002}{2001}+\frac{2001}{2002}\)và \(B=\frac{2000}{2001}+\frac{2001}{2002}\)
Ta nhận xét thấy A và B cùng có chung 1 số hạng là \(\frac{2001}{2002}\)
Nên ta chỉ so sánh \(\frac{2002}{2001}\)và \(\frac{2000}{2001}\)ta so sánh 2 phân số đó với 1
Vì 2002>2001 nên \(\frac{2002}{2001}\)> 1
Vì 2000<2001 nên \(\frac{2000}{2001}\)<1
\(\Leftrightarrow\)\(\frac{2002}{2001}>\frac{2000}{2001}\)
\(\Leftrightarrow\)\(\frac{2002}{2001}+\frac{2001}{2002}>\frac{2000}{2001}+\frac{2001}{2002}\)
Vậy A>B

\(\Rightarrow2A=2+2^2+2^3+...+2^{2003}\\ \Rightarrow2A-A=2+2^2+2^3+...+2^{2003}-1-2-...-2^{2002}\\ \Rightarrow A=2^{2003}-1=B\)

B=2000/2001+2002 + 2001/2001+2002
Ta có:
2000/2001 > 2000/2001+2002
2001/2002 > 2001/2001+2002
Vậy A >B
\(B=\frac{2000}{2001}+2002+\frac{2001}{2001}+2002\)
Ta có: \(\frac{2000}{2001}>\frac{2000}{2001}+2002\)
\(\frac{2001}{2002}>\frac{2001}{2001}+2002\)
Vậy A>B

đề lạ zậy ko so sánh mà bảo so sánh!!!!!!! chả hỉu *_*!
765885
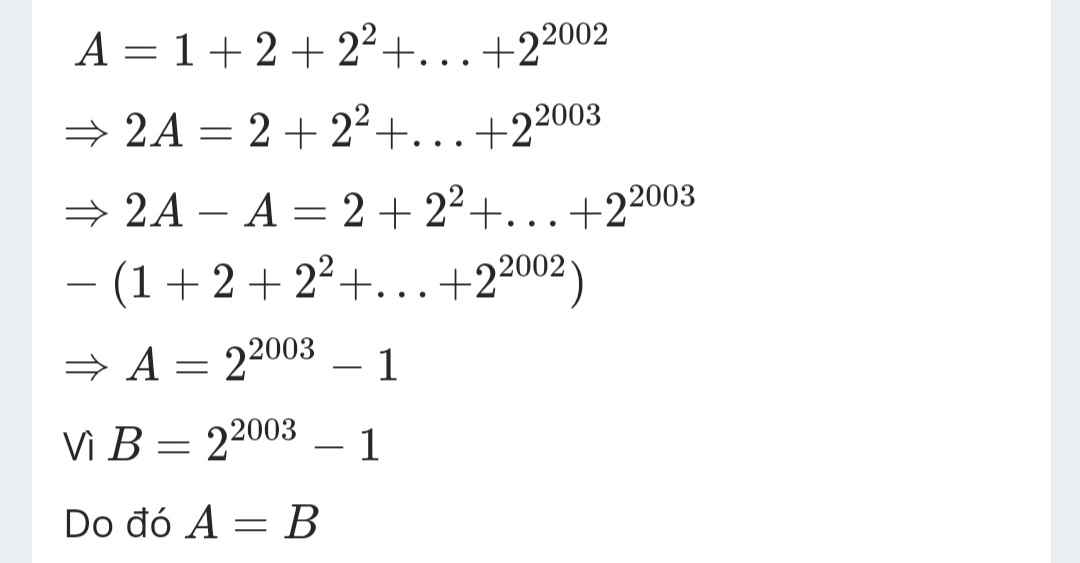
A = 2002.2002
A = (2001+1).2002
A = 2001.2002+2002
=> A<B