Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB ( đpcm)
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy ΔMON vuông tại O.
Góc 
là góc nội tiếp chắn nửa đường tròn nên 
= 900
Tứ giác AOPM có:
Suy ra, tứ giác AOPM nội tiếp đường tròn.
Xét ∆ MON và ∆ APB có:
=> Hai tam giác MON và APB đồng dạng
* Theo a, ∆MON và APB đồng dạng với nhau với tỉ số đồng dạng là:
Mà: MN = MP+NP = MA+NB = R/2 +2R = 5R/2
a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.
a: Xét tứ giác AIOC có \(\widehat{AIO}+\widehat{ACO}=180^0\)
nên AIOC là tứ giác nội tiếp
Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
hay OA⊥BC
b: Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó: ΔABD\(\sim\)ΔAEB
Suy ra: AB/AE=AD/AB
hay \(AB^2=AD\cdot AE\)
a: Xét tứ giác AIOC có \(\widehat{AIO}+\widehat{ACO}=180^0\)
nên AIOC là tứ giác nội tiếp
Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
hay OA⊥BC
b: Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó: ΔABD\(\sim\)ΔAEB
Suy ra: AB/AE=AD/AB
hay \(AB^2=AD\cdot AE\)
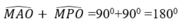
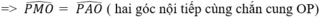
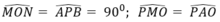
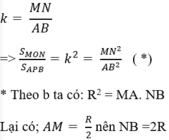
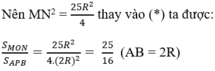
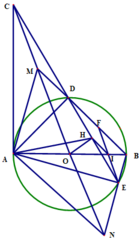
a: góc ACB=1/2*sđ cung AB=90 độ
=>BC vuông góc AM
góc ADB=1/2*sđ cung AB=90 độ
=>BD vuông góc AN tại D
ΔABM vuông tại B có BC là đường cao
nên AC*AM=AB^2
ΔABN vuông tại B có BD là đường cao
nên AD*AN=AB^2
=>AC*AM=AD*AN
=>AC/AN=AD/AM
=>ΔACD đồng dạng với ΔANM
=>góc ACD=góc ANM
=>góc DCM+góc DNM=180 độ
=>DCMN nội tiếp
b: AC*AM=AB^2=(2R)^2=4R^2
AD*AN=AB^2=(2R)^2=4R^2