Trong mặt phẳng tọa độ Oxy, đường thẳng đi qua điểm và vuông góc với đường thẳng có phương trình tổng quát là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vecto MN=(1;2)
=>VTPT là (-2;1)
Phương trình MN là:
-2(x-3)+1(y+1)=0
=>-2x+6+y+1=0
=>-2x+y+7=0
Phương trình tham số là:
x=3+t và y=-1+2t

Để đường thẳng \(y=\left(m-2\right)x+k\) song song với đường thẳng \(y=5x-1.\)
\(\Rightarrow\left\{{}\begin{matrix}m-2=5.\\k\ne-1.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=7.\\k\ne-1.\end{matrix}\right.\)
Đường thẳng \(y=\left(m-2\right)x+k\) đi qua điểm \(P\left(2;1\right).\)
\(\Rightarrow1=\left(7-2\right).2+k.\\ \Leftrightarrow1=10+k.\\ \Leftrightarrow k=-9\left(TM\right).\)
Vậy \(m=7;k=-9.\)

Vì (d)//y=2x+1 nên a=2
=>y=2x+b
Thay x=-1 và y=2 vào (d), ta được:
b-2=2
=>b=4

h bn thay x=1, y=3 vào phương trình đường thẳng (d)
tìm được m
hok tốt
Vì \(M\left(1;3\right)\in\left(d\right)\)
\(\Rightarrow3=2m+m-3\)
\(\Leftrightarrow3m=6\)
\(\Leftrightarrow m=2\)

Vì đường thẳng song song với y =3x +1 nên
\(a=3\) Vậy đường thẳng có dạng \(y=3x+b\)
Do đường thẳng đi qua điểm M nên :
\(2=3\times-1+b\Leftrightarrow b=5\)
Vậy \(\hept{\begin{cases}a=3\\b=5\end{cases}}\)

a: 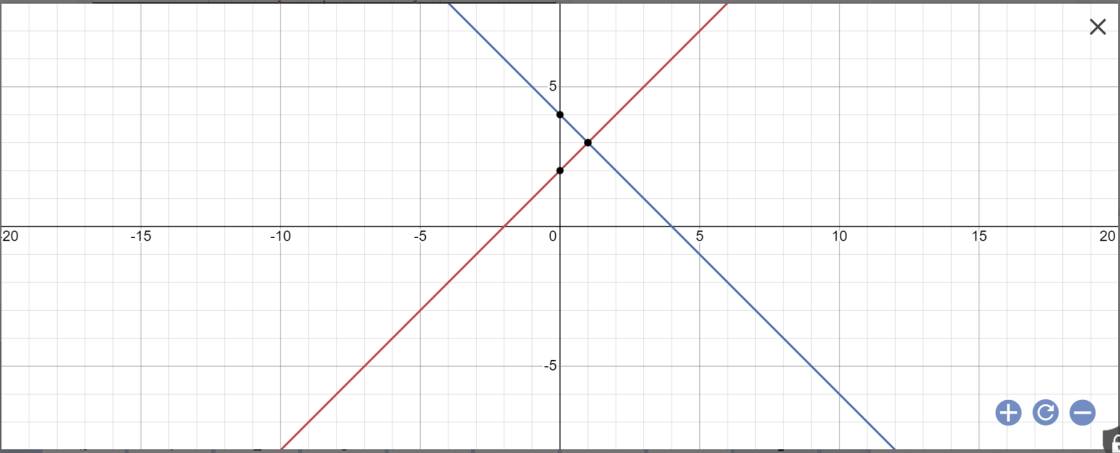
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

Thay tọa độ điểm A(0;5) vào phương trình đường thẳng d : y = m x + 5. ta được:
5=m.0+5 luôn đúng với mọi giá trị của tham số m nên đường thẳng (d) luôn
đi qua điểm A với mọi giá trị của m.

Chọn D