Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
f'(x)=y'=-3x^2+2x
f'(2)=-3*2^2+2*2=-3*4+4=-8
f(2)=-2^3+2^2-1=-8-1+4=-9+4=-5
y=f(2)+f'(2)(x-2)
=-5+(-8)(x-2)
=-8x+16-5
=-8x+11
- Hàm số đã cho xác định với ∀x ∈ R.
- ta có:
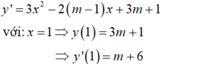
- Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là:
y = (m+ 6)(x – 1) + 3m + 1
- Tiếp tuyến này đi qua A(2; - 1) nên có:
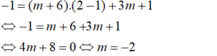
- Vậy m = -2 là giá trị cần tìm.
Chọn A.
Ta có: y’ = 3x2 – 4x + 2.
Tiếp tuyến tại M, N của (C) vuông góc với đường thẳng y = -x + 2017. Nên tiếp tuyến tại M và N có hệ số góc là 1
Hoành độ x1, x2 của các điểm M, N là nghiệm của phương trình 3x2 – 4x + 2 = 1.
Suy ra x1 + x2 = 4/3 ( hệ thức Vi-et).
Đáp án C
y ' = 3 x 2 − 4 x + 2
Do tại các điểm M, N tiếp tuyến với vuông góc với đường thẳng y = − x + 2018
nên
3 x 2 − 4 x + 2 . − 1 = − 1 ⇔ 3 x 2 − 4 x + 1 = 0 ⇔ x = 1 x = 1 3
Suy ra x 1 + x 2 = 1 + 1 3 = 4 3 .
I. Hàm số xác định trên D = R.
+) \(\lim\limits f\left(x\right)_{x\rightarrow1}=\lim\limits_{x\rightarrow1}\dfrac{x^2-3x+2}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-2\right)\left(x-1\right)}{\left(x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\left(x-2\right)\)
\(=-1\)
+) \(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\left(1-2x\right)=-1\)
=> Hàm số liên tục tại x0 = 1
II. Gọi phương trình tiếp tuyến tại N(x0; y0) là:
y = y'(x0)(x - x0) + y0
y = -x3 - x2 - 6x + 1
=> y' = -3x2 - 2x + 6
Vì tiếp tuyến song song với đường thẳng y = -6x + 17 => y'(x0) = 6
<=> -3x2 - 2x + 6 = 6
<=> -3x2 - 2x = 0
<=> -x(3x + 2) = 0
<=> x = 0 hoặc x = -2/3
Trường hợp 1: x0 = 0 => y0 = 0
=> y'(x0) = 6
=> Phương trình tiếp tuyến: y = 6(x - 0) + 1
<=> y = 6x + 1
Trường hợp 2: x0 = -2/3 => y0 = 37/9
=> y'(x0) = 9
=> Phương trình tiếp tuyến: y = 9(x + 2/3) + 37/9
<=> y = 9x + 91/9
- Tiếp tuyến (d) tại điểm M của đồ thị (C) có hoành độ x 0 = 0 ⇒ y 0 = 3 .
- Ta có:
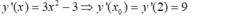
- Phương trình tiếp tuyến (d) tại điểm M của đồ thị (C) là:
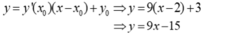
- Xét phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm phương trình :
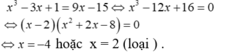
- Với x = -4 thì y = 9.(-4) – 15 = -51.
- Vậy N(- 4 ; -51) là điểm cần tìm.
Chọn C.
Đáp án D
y ' = 3 x 2 − 1 ⇒ y ' 1 = 3 .1 2 − 1 = 2
Phương trình tiếp tuyến của (C) tại điểm M(1;2) là: y = y ' 1 . x − 1 + 2 hay y = 2x.
Với x 0 = 1 thì y 0 = 2016 và f’(1) = 0.
- Do đó, phương trình tiếp tuyến tại điểm có hoành độ x= 1 là
y = 0(x- 1) + 2016 hay y = 2016.
+ Đường thẳng ∆ đi qua điểm M( -1; -2) có hệ số góc k có dạng ∆: y= k( x+ 1) -2 .
+ ∆ là tiếp tuyến của (C ) khi và chỉ khi hệ sau có nghiệm:
x 3 - x 2 + x + 1 = k ( x + 1 ) - 2 ( 1 ) 3 x 2 - 2 x + 1 = k ( 2 )
+Thay (2) vào (1) ta được
x3- x2+ x+ 1= ( 3x2- 2x+1) (x+1) -2
Hay ( x+ 1) 2(x-1) =0
Suy ra x= -1 ( trùng với M nên loại ) hoặc x= 1
Với x= 1 thì y= 2. Vậy N( 1;2)
Chọn C.