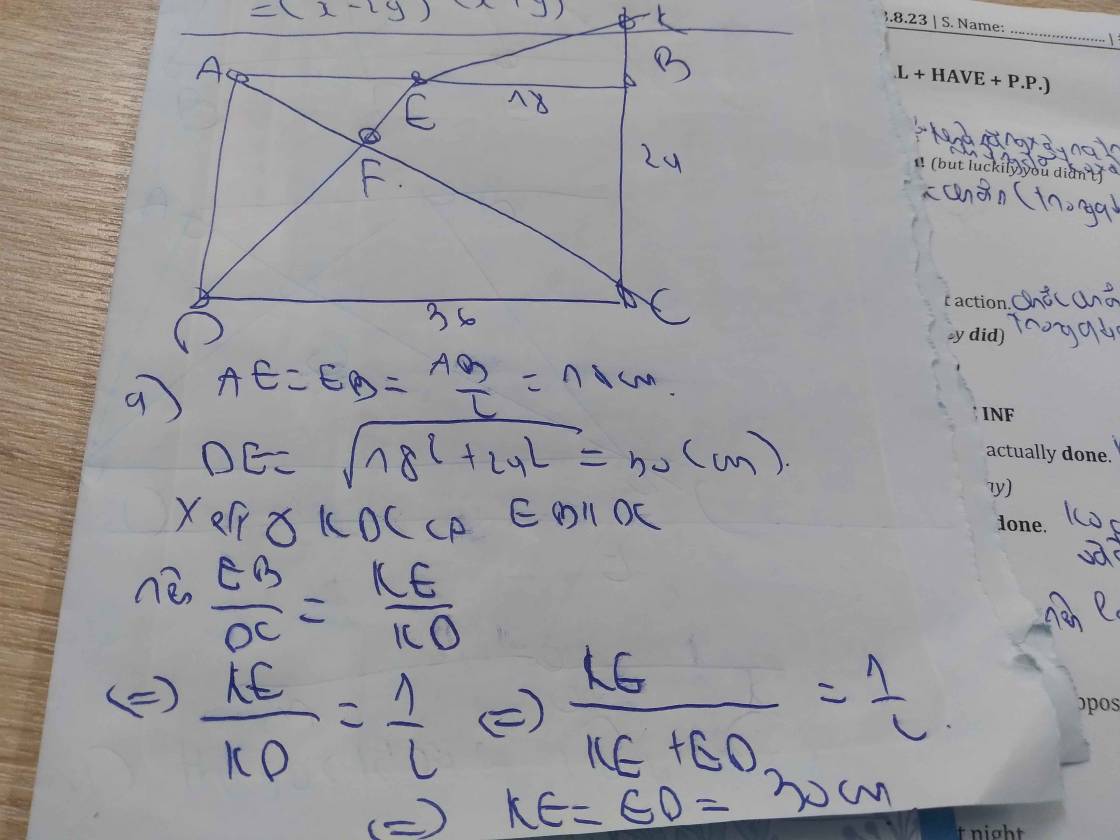
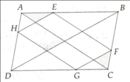
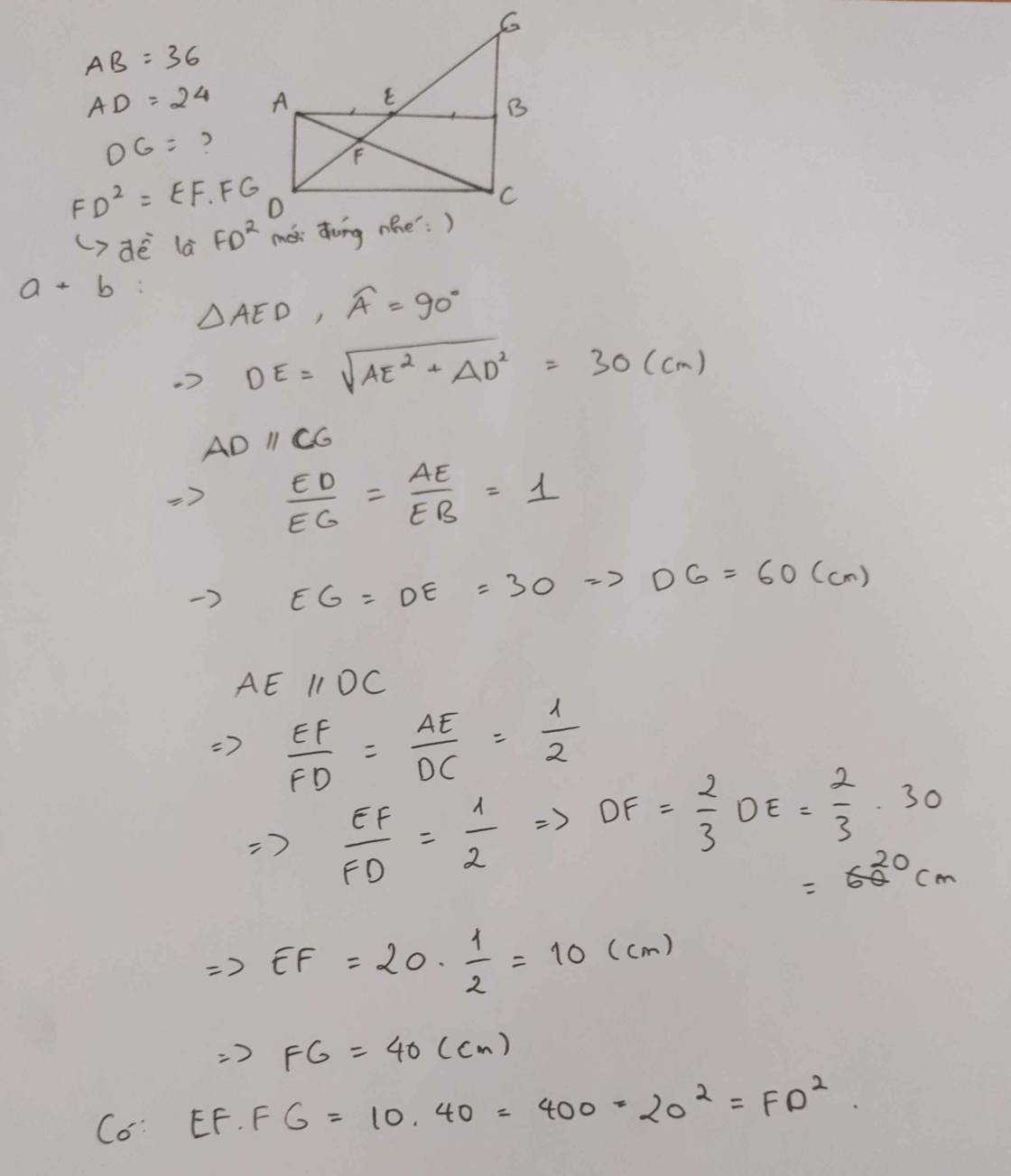Cho hình bình hành ABCD, E là điểm bất kì trên cạnh AB ( E≠A, E≠B ). Tia DE cắt AC ở F, cắt CB ở G.
a) Chứng minh ∆AEFđồng dạng ∆CDF; ∆AFDđồng dạng ∆CFG.
b) Chứng minh FD2 = FE.FG.
c) Từ F kẻ đường thẳng song song với đường thẳng AB cắt AD tại điểm H. Chứng minh 1:AE+1:AB=1:HF