Biết a,b,c dương; a + b + c = 1. Chứng minh: \(\frac{a+b^2}{b+c}+\frac{b+c^2}{c+a}+\frac{c+a^2}{a+b}\)\(\ge\)\(2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
1
13 tháng 1 2016
Theo bài ra. ta có: a x b = c => b = c : a (1) thế vào b x c = 4 x a
Có: c : a x c = 4 x a => c2 = 4 x a2 (2)
a x c = 9 x b => a x c = 9 x c : a => a2 = 9 => a = 3 (a dương)
a = 3 thì (2) <=> c2 = 4 x a2 = 5 x 32 = 36 = 62 => c = 6 (c dương)
Thế vào (1) có: b = c : a = 6 : 3 = 2
Vậy a = 3 ; b = 6 và c = 2
CM
11 tháng 7 2019
Đáp án D.
Ta có I = ∫ 1 2 d x x x + 1 x + 1 + x
Lại có:
x + 1 + x x + 1 − x = 1 ⇒ I = ∫ 2 2 x + 1 − x x x + 1 d x = ∫ 1 2 1 x − 1 x + 1 d x
= 2 x − 2 x + 1 2 1 = 4 2 − 2 3 − 2 = 32 − 12 − 2 ⇒ a = 32 ; b = 12 ; c = 2
Vậy a + b + c = 46.
CM
6 tháng 5 2018
∫ 1 2 d x x + 1 x + x x + 1 = ∫ 1 2 d x x . x + 1 x + 1 + x = ∫ 1 2 x + 1 - x x . x + 1 x + 1 2 d x = ∫ 1 2 x + 1 - x x + 1 . x d x = ∫ 1 2 d x x - ∫ 1 2 d x x + 1 = 2 x - 2 x + 1 1 2 = 4 2 - 2 3 - 2 - 32 - 12 - 2 ⇒ a = 32 b = 12 c = 2
Đáp án cần chọn là D
KT
1
DA
1 tháng 4 2018
Vì a,b,c dương nên: \(a^3>b^3\Rightarrow a>b\left(1\right)\)
\(a^3>c^3\Rightarrow a>c\left(2\right)\)
Cộng (1) và (2),ta được: 2a>b+c
\(\Rightarrow4a>2\left(b+c\right)\)
\(\Rightarrow4a>a^2\)
\(\Rightarrow4>a\)
Mà a là số chẵn, nên: a=2
Vì a>b>c,nên: 2>b>c ; b=1,c=1
Vậy a,b,c cần tìm lần lượt là 2,1,1
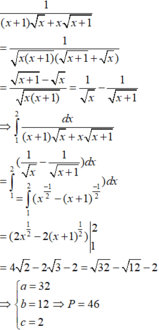
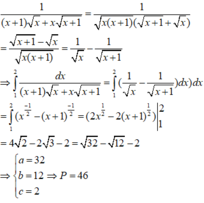
\(VT=\left(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\right)+\left(\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^2}{a+b}\right)\)
\(=A+B\)
\(A=\frac{a}{b+c}+1+\frac{b}{c+a}+1+\frac{c}{a+b}+1-3=\left(a+b+c\right)\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)-3\)
\(\ge\left(a+b+c\right).\frac{9}{2\left(a+b+c\right)}-3=\frac{3}{2}\)
\(B=\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^2}{a+b}\ge\frac{\left(a+b+c\right)^2}{b+c+c+a+a+b}=\frac{a+b+c}{2}=\frac{1}{2}\)
\(A+B\ge\frac{3}{2}+\frac{1}{2}=2\)
Biểu thức B có lệch 1 chút, nhưng vẫn áp dụng bất đẳng thức \(\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\ge\frac{\left(x+y+z\right)^2}{a+b+c}\) và vẫn ra kết quả như trên.