Trong không gian Oxyz, cho ba đường thẳng Đường thẳng
d
:
x
1
=
y
1
=
z
+
1
-
2
;
∆
1
=
x
-
3
2
=
y
1
=
z
-
1
1
;
∆
2
:
x
-
1
1
=
y
-
2
2
=
z
1
. Đường thẳng
∆
vuông góc với d đồng thời...
Đọc tiếp
Trong không gian Oxyz, cho ba đường thẳng Đường thẳng d : x 1 = y 1 = z + 1 - 2 ; ∆ 1 = x - 3 2 = y 1 = z - 1 1 ; ∆ 2 : x - 1 1 = y - 2 2 = z 1 . Đường thẳng ∆ vuông góc với d đồng thời cắt ∆ 1 ; ∆ 2 tương ứng tại H , K sao cho độ dài HK nhỏ nhất. Biết rằng ∆ có một vecto chỉ phương u → h ; k ; 1 .Giá trị của h - k bằng:
A. 0
B. 4
C. 6
D. -2
. Phương trình mặt phẳng (α) là x+y+z-1=0. 
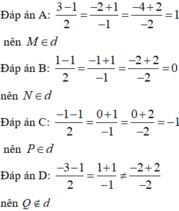
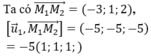
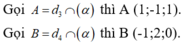
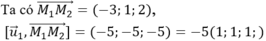
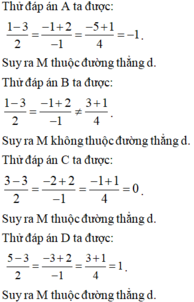
Giả sử
ta có:
Đường thẳng d có 1 VTCP là u d → 1 ; 1 ; - 2
Vì
Suy ra đường thẳng ∆ nhận u → 1 ; 1 ; 1 là 1 VTCP h = k = 1
Vậy h - k = 1 - 1 = 0
Chọn A.