Cho ba đường thẳng (d1):y=1/2x-3; (d2): y=3-2x và (d3): y = - 7/6 x + 1
a.Chứng minh ba đường thẳng này đồng quy tại điểm A.
b. Tính chu vi và diện tích tam giác có đỉnh là A, hai đỉnh còn lại lần lượt là giao của (d1) và (d2) với trục tung.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 4 2017
Giao điểm A(x; y) của hai đường thẳng d 2 và d 3 là nghiệm hệ phương trình: y = - x + 3 y = - 2 x + 1 ⇔ x = - 2 y = 5 ⇒ A ( - 2 ; 5 )
Do đường thẳng d 4 // d 1 nên d 4 có dạng: y = 2x + b
Ba đường thẳng d 2 ; d 3 ; d 4 đồng quy nên điểm A(-2; 5) thuộc đường thẳng d 4 .
Suy ra: 5 = 2.(-2) + b ⇔ b = 9
Vậy phương trình đường thẳng ( d 4 ) là y = 2x + 9.
30 tháng 10 2023
Tọa độ giao điểm của (d1) và (d2) là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}2x+1=x+2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-x=2-1\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
Để (d1),(d2),(d3) đồng quy thì (d3) đi qua A(1;3)
Thay x=1 và y=3 vào (d3), ta được:
\(m^2+1+m=3\)
=>\(m^2+m-2=0\)
=>\(m^2+2m-m-2=0\)
=>\(\left(m+2\right)\left(m-1\right)=0\)
=>\(\left[{}\begin{matrix}m+2=0\\m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=1\end{matrix}\right.\)
help me pls9 tháng 1 2022
1: Để hai đường song song thì m+3=2
hay m=-1
3: Tọa độ của điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\2x+4=0\end{matrix}\right.\Leftrightarrow A\left(-2;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}y_B=0\\-x+4=0\end{matrix}\right.\Leftrightarrow B\left(4;0\right)\)
CM
19 tháng 3 2018
Đáp án C
Hoành độ giao điểm của d 1 và d 2 là nghiệm phương trình:
2x + 1 = x -1 nên x = -2
Với x = -2 thì y = 2. (-2) + 1 = -3
Vậy 2 đường thẳng d 1 và d2 cắt nhau tại A(-2; -3).
Để ba đường thẳng đã cho đồng quy thì điểm A(-2; -3) thuộc đồ thị hàm số y = (m + 1)x – 2
Suy ra: -3 = (m + 1).(-2) - 2
CM
18 tháng 3 2019
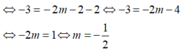
Đáp án B
+Giao điểm của d1 và d2 là nghiệm của hệ:
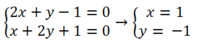
Vậy 2 đường thẳng d1 và d2 tại A( 1 ; -1) .
+Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên tọa độ A thỏa phương trình d3
Suy ra : m+ 1-7= 0 hay m= 6.
CM
6 tháng 10 2019
Chọn B.
Gọi M(xM; yM) là giao điểm của d1 và d2. Khi đó, tọa độ giao điểm M của d1 và d2 là nghiệm của hệ phương trình:
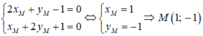
Để 3 đường thẳng d1, d2, d3 đồng quy thì M(1;-1) ∈ (d3): mx - y - 7 = 0, nên ta có:
m.1 - (-1) - 7 = 0 ⇔ m + 1 - 7 = 0 ⇔ m - 6 = 0 ⇔ m = 6
Vậy 3 đường thẳng d1, d2, d3 đồng quy.
8 tháng 9 2021
Bài 3:
Vì (d)//(d1) nên a=3
Vậy: (d): y=3x+b
Thay \(x=\dfrac{2}{3}\) và y=0 vào (d), ta được:
\(b+2=0\)
hay b=-2
CM
19 tháng 1 2017
+) Thay tọa độ điểm A (2; 1) vào phương trình đường thẳng d1 ta được:
1 = − 2 . 2 ⇔ 1 = − 4 (vô lý) nên A ∉ d 1 hay A (2; 1) không là giao điểm của d1 và d3. Suy ra A sai.
+) Thay tọa độ điểm B (1; 4) vào phương trình đường thẳng d2 ta được:
4 = − 3 . 1 − 4 ⇔ 4 = − 4 (vô lý) nên B ∉ d 2 . Suy ra C sai
+) Xét tính đồng quy của ba đường thẳng:
* Phương trình hoành độ giao điểm của d 1 v à d 2 : − 2 x = − 3 x − 1 ⇔ x = − 1 ⇒ y = − 2 . ( − 1 ) ⇔ y = 2
Suy ra tọa độ giao điểm của d 1 v à d 2 là: (−1; 2)
* Thay x = − 1 ; y = 2 vào phương trình đường thẳng d3 ta được 2 = − 1 + 3 ⇔ 2 = 2 (luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm M (−1; 2)
Đáp án cần chọn là: D