Cho đường tròn (C1): (x-1)2+ (y-2)2=4; (C2): x2+ y2-8x+4y+11=0 Số tiếp tuyến chung của (C1), (C2) là
A. 1
B. 2
C. 3
D. 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
14 tháng 1 2017
Đúng(0)
Những câu hỏi liên quan
CM
15 tháng 1 2017
Đường tròn (C1) có tâm và bán kính: I1=(0;0), và R1= 2; (C2) có tâm I2 (-10; 16) và bán kính R2= 1; khoảng cách giữa hai tâm .
Vậy 2 đường tròn đã cho không có điểm chung.
Chọn B.
CM
3 tháng 12 2017
Đáp án C.
Phép tinh tiến không làm thay đổi bán kính đường tròn nên đường tròn (C3) là ảnh của (C) qua phép tịnh tiến.
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 3 2023
Phương trình giao điểm hai đường tròn:
\(\left\{{}\begin{matrix}x^2+y^2=8\\\left(x-2\right)^2+y^2=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=8\\x^2+y^2-4x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2=8\\4x=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=\pm\sqrt{8-x^2}\\x=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}A\left(2;2\right)\\B\left(2;-2\right)\end{matrix}\right.\)
Tới đây dễ dàng viết được pt AB có dạng: \(x-2=0\)
CM
9 tháng 7 2017
Đáp án B
- Ta có (C1) với tâm I(5; -12) và R= 15.
(C2) có tâm J( 1;2) và R’ =5 .
Gọi d là tiếp tuyến chung có phương trình: ax+ by+ c= 0 ().
- Khi đó ta có :
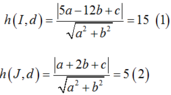
- Từ (1) và (2) suy ra :
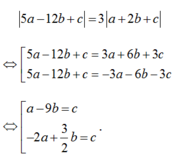
Thay vào (1):
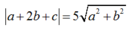
Ta có hai trường hợp :
- Trường hợp : c = a-9b thay vào (1):
(2a- 7b)2= 25 (a2+ b2)
hay 21a2+ 28ab -24b2= 0
Suy ra :
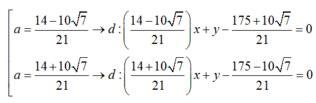
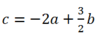
(1) => ( 7b- 2a)2=100(a2+b2) hay 96a2+ 28ab + 51b2= 0
Vô nghiệm.
Vậy 2 đường tròn đã cho có 2 tiếp tuyến chung.
CM
31 tháng 1 2018
Đường tròn (C1): x2+ y2 – 4= 0 có tâm O(0; 0) bán kính R= 2;
Đường tròn (C2) ( x -8) 2+ (y- 6)2= 4 có tâm I( 8; 6) bán kính R= 2.
Mà OI = 8 2 + 6 2 = 10
Ta thấy: OI> 2+2 nên 2 đường tròn đã cho không cắt nhau.
Chọn A.