Cho hình chữ nhật ABCD có B (-1;5). Gọi E\(\left(\frac{3}{5};\frac{9}{5}\right)\) là hình chiếu vuông góc của A trên BD và điểm G thuộc CD sao cho góc ECD = góc CBG. Biết điểm C có hoành độ nguyên, tìm tọa độ các đỉnh của hình chữ nhật.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2021
diện tích hình chữ nhật là : 12*24=288(cm2)
chiều cao bằng chiều rộng
chiều dài bằng đáy hình tam giác
Diện tích hình tam giác là: 288:2=144(cm2)
Đáp số : 144 cm2
10 tháng 1 2023
a. Ta có mỗi hình tam giác có được từ đề bài là: tam giác AED, tam giác EDC và tam giác ECB, tam giác ADC và tam giác BDC.
Diện tích tam giác AED là:
\(\dfrac{1}{2}.AD.AE=\dfrac{1}{2}.4.2=4\) cm vuông
Diện tích tam giác EBC là:
\(\dfrac{1}{2}.4.3=6\) cm vuông
Với tam giác EDC ta kẻ đường cao EH xuống DC
=> EH = BC = 4 cm
DC = AB = 2 + 3 = 5 cm
Diện tích tam giác EDC là:
\(\dfrac{1}{2}.4.5=10\) cm vuông
Diện tích tam giác ADC là:
\(\dfrac{1}{2}.AD.DC=\dfrac{1}{2}.4.5=10\) cm vuông
Diện tích tam giác ABC là:
\(\dfrac{1}{2}.BC.DC=\dfrac{1}{2}.4.5=10\) cm vuông
b. Diện tích hcn ABCD là: 4 x 5 = 20 cm vuông
Mà diện tích tam giác EDC là: 10 cm vuông
=> Tỉ số diện tích của hình tam giác EDC và diện tích hcn ABCD là:
\(\dfrac{10}{20}=\dfrac{1}{2}\)
AM
13 tháng 2 2022
Ta có: \(DM=\dfrac{1}{4}DC\) nên \(BM=\dfrac{3}{4}DC\) hay \(DC=\dfrac{4}{3}BM\)
Diện tích tam giác BCM là: \(S_{BCM}=BC\times BM:2=12\left(cm^2\right)\)
Diện tích hình chữ nhật ABCD là: \(S_{ABCD}=BC\times CD:2=BC\times\dfrac{4}{3}BM:2=\dfrac{12\times4}{3}=16\left(cm^2\right)\)
22 tháng 9 2023
a) 48cm2 trong đề bài tương ứng với diện tích của phần được mở rộng, gồm chiều dài là chiều dài hình vuông và chiều rộng là 1/3 chiều dài hình vuông. Do đó chiều dài hình vuông nhân với chính nó, hay diện tích hình vuông là:
48 : 1/3 = 144 (cm2)
Vì 12 x 12 = 144 nên chiều dài hình vuông là 12cm.
Chu vi hình vuông là:
12 x 4 = 48 (cm)
b) Diện tích của hình chữ nhật đó là:
144 x 8/9 = 128(cm2)
Nửa chu vi của hình chữ nhật đó là:
48 : 2 = 24 (cm)
Do đó chiều dài và chiều rộng lần lượt là hai số tự nhiên a và b sao cho a + b = 24 và a x b = 128.
Dễ thấy a = 24 - b = 128 : b, suy ra b = 8, a = 24 - 8 = 16.
Vậy chiều dài và chiều rộng của hình chữ nhật đó lần lượt là 16cm và 8cm.
29 tháng 1 2024
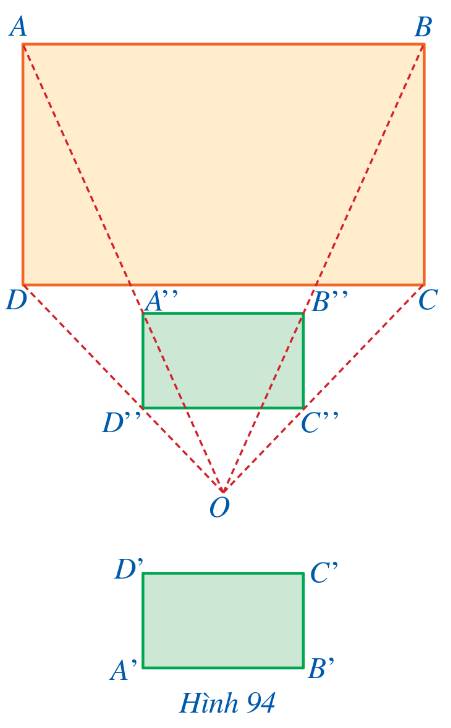
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau
12 tháng 2 2019
a,Diện tích hình vuông ABCD là:
48 x 3 = 144 (cm2)
Ta có 12 x 12 = 144
Chu vi hình ABCD là
12 x 4 = 48 (cm)
b,Diện tích hình chữ nhật đó là
144 : 9 x 8 = 128(cm2)
Tổng của chiều dài và chiều rộng là
48 : 2 = 24 (cm)
Vậy hai số có tổng là 24 và tích là 128 là 16 và 8
Đáp số:a,48 cm
b,Chiều dài:16
Chiều rộng:8
CM
7 tháng 2 2018
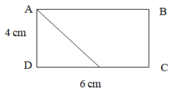
a) Hình bên có: 4 góc vuông, 3 góc nhọn, 1 góc tù.
b) Chu vi hình chữ nhật ABCD là : (4+6) x 2 = 20 cm.