Tìm x, biết:
\(\begin{array}{l}a)x + 7,25 = 15,75;\\b)\left( { - \frac{1}{3}} \right) - x = \frac{{17}}{6}\end{array}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\begin{array}{l}a)x + 0,25 = \frac{1}{2}\\x = \frac{1}{2} - 0,25\\x = \frac{1}{2} - \frac{1}{4}\\x = \frac{2}{4} - \frac{1}{4}\\x = \frac{1}{4}\end{array}\)
Vậy \(x = \frac{1}{4}\)
\(\begin{array}{l}b)x - \left( { - \frac{5}{7}} \right) = \frac{9}{{14}}\\x = \frac{9}{{14}} + \left( { - \frac{5}{7}} \right)\\x = \frac{9}{{14}} + \left( { - \frac{{10}}{{14}}} \right)\\x = \frac{{ - 1}}{{14}}\end{array}\)
Vậy \(x = \frac{{ - 1}}{{14}}\)

\(\begin{array}{l}a)\sqrt x - 16 = 0\\\sqrt x = 16\\x = {16^2}\\x = 256\end{array}\)
Vậy x = 256
\(\begin{array}{l}b)2\sqrt x = 1,5\\\sqrt x = 1,5:2\\\sqrt x = 0.75\\x = {(0,75)^2}\\x = 0,5625\end{array}\)
Vậy x = 0,5625
\(\begin{array}{l}c)\sqrt {x + 4} - 0,6 = 2,4\\\sqrt {x + 4} = 2,4 + 0,6\\\sqrt {x + 4} = 3\\x + 4 = 9\\x = 5\end{array}\)
Vậy x = 5

\(\begin{array}{l}a)2x + \frac{1}{2} = \frac{7}{9}\\2x = \frac{7}{9} - \frac{1}{2}\\2x = \frac{{14}}{{18}} - \frac{9}{{18}}\\2x = \frac{5}{{18}}\\x = \frac{5}{{18}}:2\\x = \frac{5}{{18}}.\frac{1}{2}\\x = \frac{5}{{36}}\end{array}\)
Vậy \(x = \frac{5}{{36}}\)
\(\begin{array}{l}b)\frac{3}{4} - 6x = \frac{7}{{13}}\\ 6x = \frac{3}{{4}} - \frac{7}{13}\\ 6x = \frac{{39}}{{52}} - \frac{{28}}{{52}}\\ 6x = \frac{{11}}{{52}}\\x = \frac{{11}}{{52}}:6\\x = \frac{{11}}{{52}}.\frac{{1}}{6}\\x = \frac{{11}}{{312}}\end{array}\)
Vậy \(x = \frac{{11}}{{312}}\)

\(\begin{array}{l}a)x - \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right) = \dfrac{9}{{20}}\\x = \dfrac{9}{{20}} + \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right)\\x = \dfrac{9}{{20}} + \dfrac{{25}}{{20}} - \dfrac{{28}}{{20}}\\x = \dfrac{{6}}{{20}}\\x = \dfrac{{ 3}}{{10}}\end{array}\)
Vậy \(x = \dfrac{{ 3}}{{10}}\)
\(\begin{array}{*{20}{l}}{b)9 - x = \dfrac{8}{7} - \left( { - \dfrac{7}{8}} \right)}\\\begin{array}{l}9 - x = \dfrac{8}{7} + \dfrac{7}{8}\\9 - x = \dfrac{{64}}{{56}} + \dfrac{{49}}{{56}}\\9 - x = \dfrac{{113}}{{56}}\end{array}\\{x = 9 - \dfrac{{113}}{{56}}}\\{x = \dfrac{{504}}{{56}} - \dfrac{{113}}{{56}}}\\{x = \dfrac{{391}}{{56}}}\end{array}\)
Vậy \(x = \dfrac{{391}}{{56}}\)

a) Hệ \(\left\{ \begin{array}{l}x < 0\\y \ge 0\end{array} \right.\) gồm hai bất phương trình bậc nhất hai ẩn là \(x < 0\) và \(y \ge 0\)
=> Hệ trên là hệ bất phương trình bậc nhất hai ẩn.
b) Hệ \(\left\{ \begin{array}{l}x + {y^2} < 0\\y - x > 1\end{array} \right.\) không là hệ bất phương trình bậc nhất hai ẩn vì \(x + {y^2} < 0\) không là bất phương trình bậc nhất hai ẩn (chứa \({y^2}\))
c) Hệ \(\left\{ \begin{array}{l}x + y + z < 0\\y < 0\end{array} \right.\) không là hệ bất phương trình bậc nhất hai ẩn vì \(x + y + z < 0\) có 3 ẩn không là bất phương trình bậc nhất hai ẩn.
d) Ta có:
\(\left\{ \begin{array}{l} - 2x + y < {3^2}\\{4^2}x + 3y < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2x + y < 9\\16x + 3y < 1\end{array} \right.\)
Đây là hệ bất phương trình bậc nhất hai ẩn và gồm hai bất phương trình bậc nhất hai ẩn là \( - 2x + y < 9\) và \(16x + 3y < 1\)

Ta thấy hệ \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn với các bất phương trình bậc nhất hai ẩn là \(x - y < 0;2y \ge 0\).
=> Chọn A.
Đáp án B loại vì \(3x + {y^3} < 0\) chứa \(y^3\).
Đáp án C loại vì \({y^2} + 3 < 0\) chứa \(y^2\).
Đáp án D loại vì \( - {x^3} + y < 4\) chứa \(x^3\).

\(\begin{array}{l}A \cap B = \{ 0\} \\A \cup B = \mathbb{R}\end{array}\)

Tham khảo:
a) Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
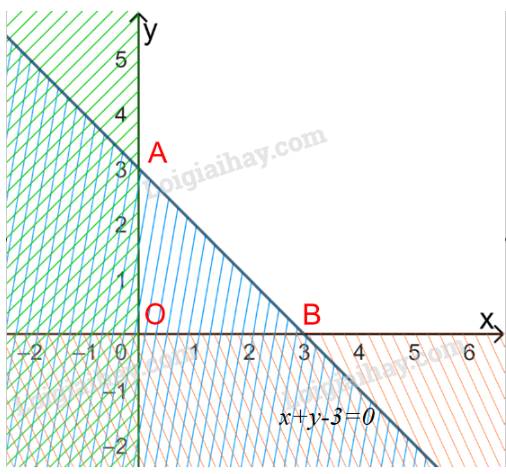
Miền không gạch chéo (bao gồm cạnh AB, tia Ay, Bx) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
b) Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
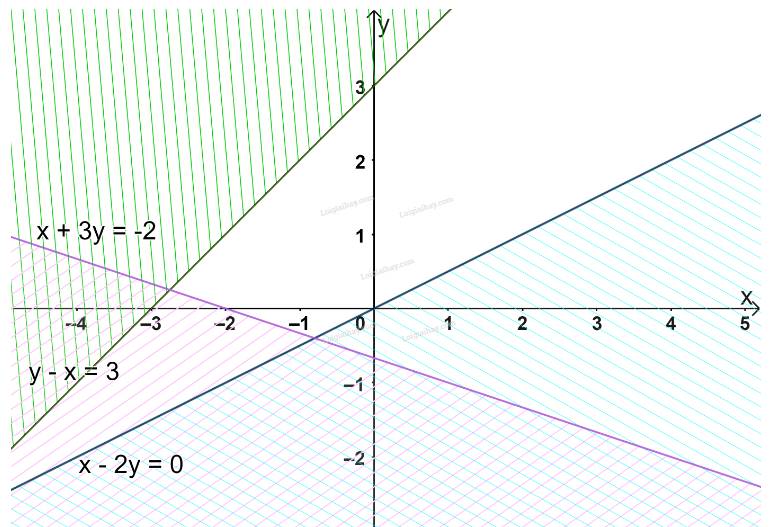
Miền không gạch chéo (không bao gồm cạnh, các bờ) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
c) Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy.
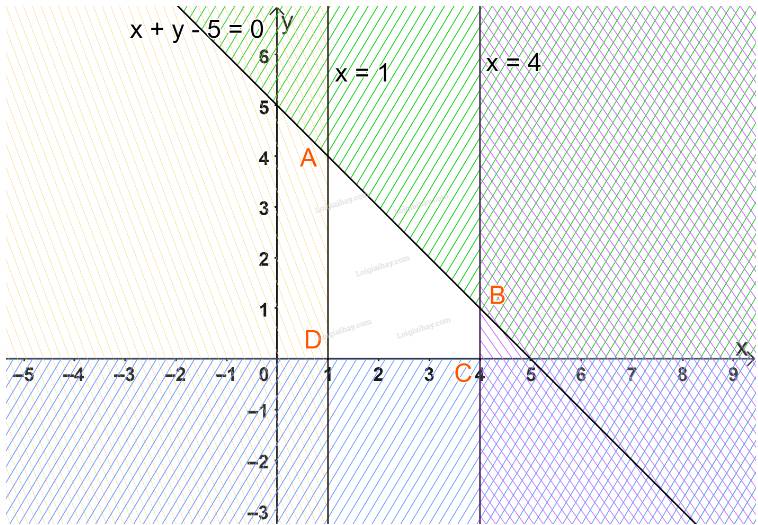
Miền không gạch chéo (miền tứ giác ABCD, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
\(\begin{array}{l}a)x + 7,25 = 15,75\\x = 15,75 - 7,25\\x = 8,5\end{array}\)
Vậy x = 8,5
\(\begin{array}{l}b)\left( { - \frac{1}{3}} \right) - x = \frac{{17}}{6}\\\left( { - \frac{1}{3}} \right) - \frac{{17}}{6} = x\\\frac{{ - 2}}{6} - \frac{{17}}{6} = x\\\frac{{ - 19}}{6} = x\\x = \frac{{ - 19}}{6}\end{array}\)
Vậy \(x = \frac{{ - 19}}{6}\)
Chú ý: A = B và B = A là tương đương nhau