Tìm các số vừa thuộc Ư(300) vừa thuộc về B(25)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,2025-\left(2023-2022\right)^{2024}+\left(2024+1\right)^0\\ =2025-1^{2024}+2025^0\\ =2025-1+1\\ =2025\\ b,?\)
Nhìn đề câu b không hiểu bạn
`a, 2025 - (2023 - 2022)^2024+(2024+1)^0`
`= 2025 - 1^2024 + 2025^0`
`= 2025 - 1 +1`
`= 2024+1`
`=2025`
`b, (2^7)/13 . 3/(2^7)+ (2^10)/14 . 1/(2^6)`
`= 13/3+ (2^6 . 2^4)/14 . 1/(2^6)`
`= 13/3 + (2^4)/14`
`=13/3 + 16/14`
`= 115/21`

Ta có:
`14a + 21b + 5a - 2b`
`= (14a + 5a)+(21b - 2b)`
`= 19a + 19b`
`= 19. (a + b)`
`= 19 . 100`
`= 1900`
Vậy: `14a + 21b + 5a - 2b = 1900` với `a+b=100`


11) Ta có:
`9^5=(3^2)^5=3^10`
`27^3=(3^3)^3=3^9`
Vì: `9<10=>3^9<3^10`
`=>9^5>27^3`
12) Ta có:
`3^500=(3^5)^100=243^100`
`7^300=(7^3)^100=343^100`
Vì: `243<343=>243^100<343^100`
`=>3^500<7^300`
13) Ta có:
`8^5=(2^3)^5=2^15=2*2^14`
`3*4^7=3*(2^2)^7=3*2^14`
Vì: `2<3=>2*2^14<3*2^14`
`=>8^5<3*4^7`

3) x³ = 343
x³ = 7³
x = 7
4) (7x - 11)³ = 2⁵.5² + 200
(7x - 11)³ = 32.25 + 200
(7x - 11)³ = 800 + 200
(7x - 11)³ = 1000
(7x - 11)³ = 10³
7x - 11 = 10
7x = 10 + 11
7x = 21
x = 21 : 7
x = 3
6) Điều kiện: x 2019
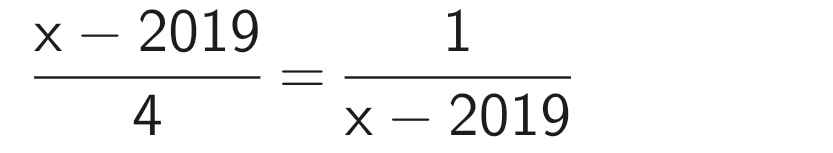
(x - 2019).(x - 2019) = 1.4
(x - 2019)² = 4
(x - 2019)² = 2² hoặc (x - 2019)² = (-2)²
x - 2019 = 2 hoặc x - 2019 = -2
*) x - 2019 = 2
x = 2 + 2019
x = 2021 (nhận)
*) x - 2019 = -2
x = -2 + 2019
x = 2017 (nhận)
Vậy x = 2017; x = 2021

Nếu p;q đều lẻ \(\Rightarrow7p\) lẻ nên \(7p+q\) là số chẵn lớn hơn 2 \(\Rightarrow\) là hợp số (không thỏa mãn)
\(\Rightarrow\) Trong số p; q phải có ít nhất 1 số chẵn
TH1: p chẵn \(\Rightarrow p=2\)
- Với \(q=3\Rightarrow7p+q=7.2+3=17\) là SNT và \(pq+11=2.3+11=17\) là SNT (thỏa mãn)
- Với \(q\ne3\Rightarrow q\) ko chia hết cho 3 \(\Rightarrow q=3k+1\) hoặc \(q=3k+2\)
+ Nếu \(q=3k+1\Rightarrow7p+q=14+3k+1=3\left(k+5\right)\) chia hết cho 3 => là hợp số (ktm)
+ Nếu \(q=3k+2\Rightarrow pq+11=2\left(3k+2\right)+11=3\left(2k+5\right)\) chia hết cho 3 => là hợp số (ktm)
TH2: q chẵn \(\Rightarrow q=2\)
- Với \(p=3\) thỏa mãn (em tự kiểm tra)
- Với \(p\ne3\Rightarrow p\) ko chia hết cho 3 nên \(p=3k+1\) hoặc \(p=3k+2\)
+ Nếu \(p=3k+1\Rightarrow7p+q=7\left(3k+1\right)+2=3\left(7k+3\right)\) chia hết cho 3=> là hợp số (ktm)
+ Nếu \(p=3k+2\Rightarrow pq+11=2\left(3k+2\right)+11=3\left(2k+5\right)\) chia hết cho 3 => là hợp số (ktm)
Vậy \(\left(p;q\right)=\left(2;3\right);\left(3;2\right)\)

E ơi đăng nhiều quá một lần khó nhận trợ giúp nha e, mình chia nhỏ bài ra nè

Bài 7:
a: \(5\cdot2^2+\left(x+3\right)=5^2\)
=>20+x+3=25
=>x+23=25
=>x=2
b: \(2^3+\left(x-3^2\right)=5^3-4^3\)
=>\(8+x-9=125-64=61\)
=>x=61+1=62
c:
\(4\left(x-5\right)-2^3=2^4\cdot3\)
=>\(4\left(x-5\right)=16\cdot3+8=8+48=56\)
=>x-5=14
=>x=19
d: \(5\left(x+7\right)-10=2^3\cdot5\)
=>5(x+7)-10=40
=>5(x+7)=50
=>x+7=10
=>x=3
Bài 3:
a: \(2^x+2^{x+3}=144\)
=>\(2^x+8\cdot2^x=144\)
=>\(9\cdot2^x=144\)
=>\(2^x=16\)
=>x=4
b: \(\left(x-5\right)^{2022}=\left(x-5\right)^{2021}\)
=>\(\left(x-5\right)^{2022}-\left(x-5\right)^{2021}=0\)
=>\(\left(x-5\right)^{2021}\left(x-5-1\right)=0\)
=>\(\left(x-5\right)^{2021}\cdot\left(x-6\right)=0\)
=>\(\left[{}\begin{matrix}x-5=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=6\end{matrix}\right.\)
c: \(\left(2x+1\right)^3=9\cdot81\)
=>\(\left(2x+1\right)^3=9^3\)
=>2x+1=9
=>2x=8
=>x=4

x(x+8)=20
=>\(x^2+8x-20=0\)
=>(x+10)(x-2)=0
=>\(\left[{}\begin{matrix}x=-10\\x=2\end{matrix}\right.\)
\(x\)(\(x+8\)) = 20
\(x^2\) + 8\(x\) = 20
\(x^2\) + 8\(x\) - 20 = 0
(\(x^2\) + 10\(x\)) - (2\(x\) + 10) = 0
\(x\)(\(x+10\)) - 2(\(x+10\)) = 0
(\(x+10\))(\(x-2\)) = 0
\(\left[{}\begin{matrix}x+10=0\\x-2=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-10\\x=2\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-10; 2}
 giúp ẻm câu 11 đến 22 với
giúp ẻm câu 11 đến 22 với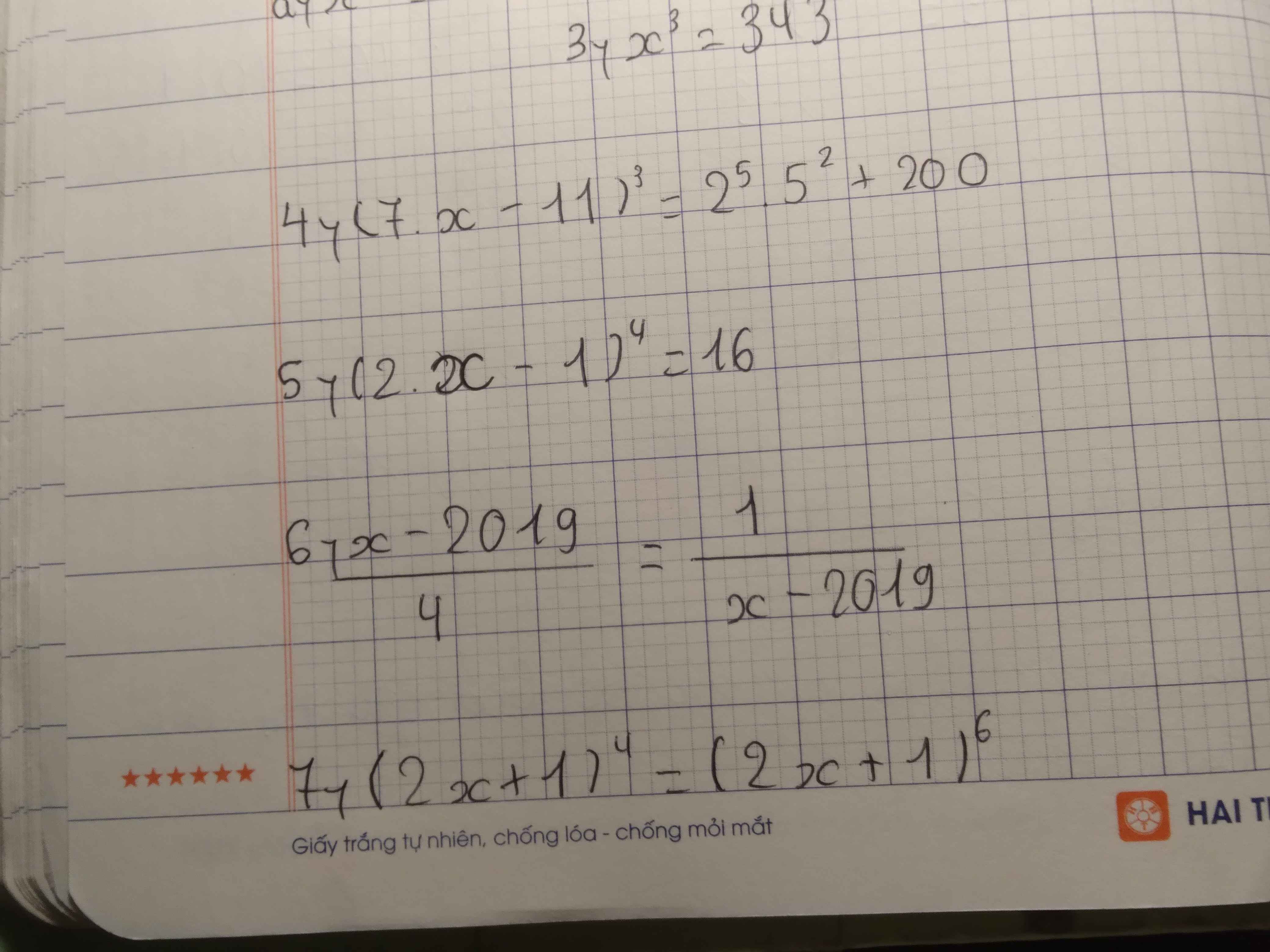


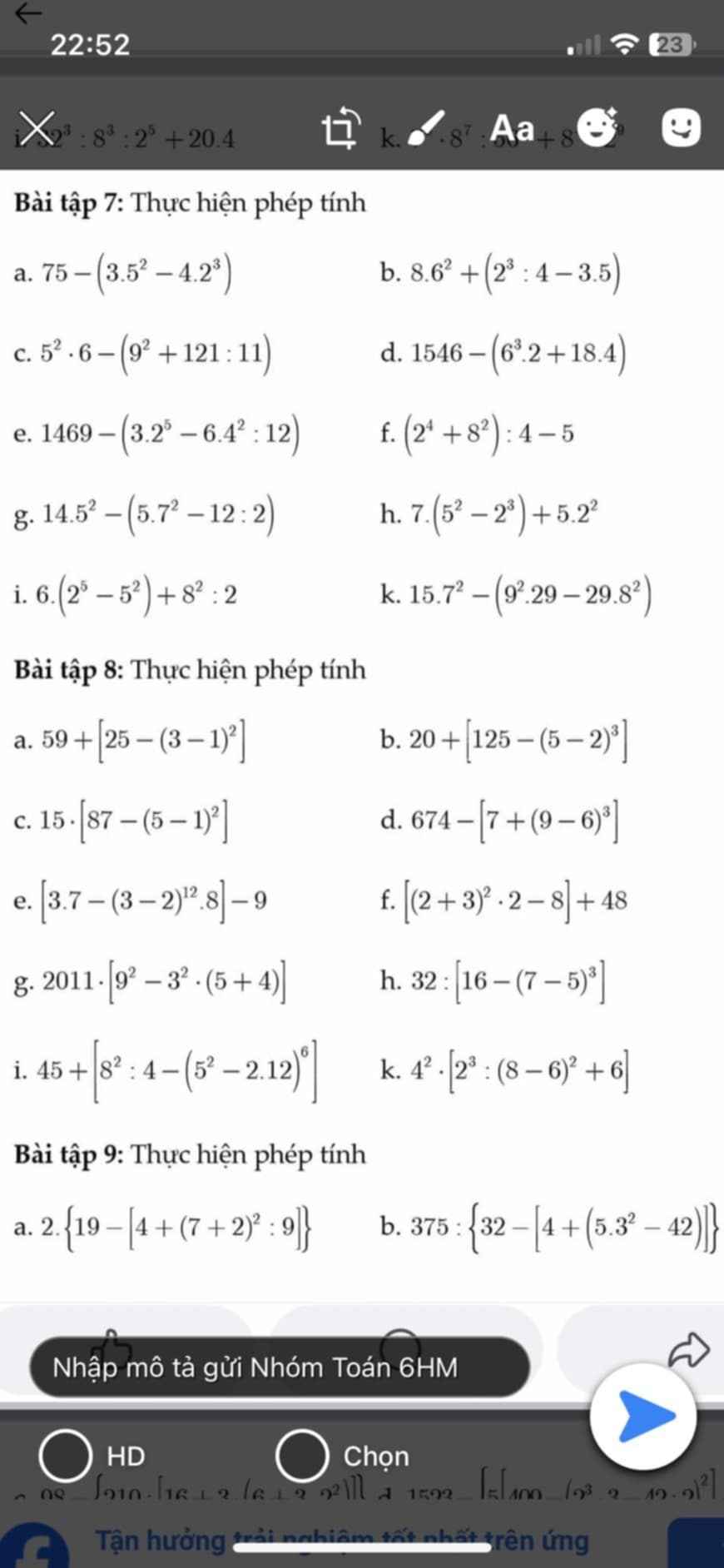

Gọi `x` là số thuộc ước của 300 và bội của 25
`=> x ⋮ 25` và `300 ⋮ x`
Ta có:
`300 = 1. 2^2 . 3 . 5^2`
Mà ` x ⋮ 25` nên `x` có dạng: `5^2 k` (`k ∈ N`*)
`=> k ∈ ` {`1 ; 2 ; 2^2 ; 3 ; 2 . 3 ; 2^2 . 3`}
`=> k ∈` {`1 ; 2 ; 4 ; 3 ; 6; 12`}
Khi đó `x ∈ {25;50;100;75;150;300}`
Ư(300) = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 200, 300}
B(25) = {1, 25, 50, 75, 100, 125, 150, 175, 200, 225, 250, 275, 300}
Vậy, các số vừa thuộc về Ư(300) vừa thuộc về B(25) là:
{25, 50, 75, 100, 150}