tìm nghiệm của đa thức : 5x+17-(2x+5)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số lượng số hạng:
(202 - 4) : 3 + 1= 67 (số hạng)
Tổng:
(202 + 4) x 67 : 2 = 6901
ĐS: ...

Tùy nha bạn
Lên lớp 10 cái đó được tính vào phần toán đại đấy

Diện tích xung quanh của căn phòng là:
\(\left(8+6\right)\times2\times4=8\times14=112\left(m^2\right)\)
Diện tích trần nhà là \(8\times6=48\left(m^2\right)\)
Diện tích cửa ra vào là 1x2,2=2,2(m2)
Diện tích 4 cửa số hình vuông là:
4x0,8x0,8=0,64x4=2,56(m2)
Diện tích cần quét vôi là:
112+48-2,2-2,56=155,24(m2)
Diện tích của tất cả cửa là:
\(1\times2,2+4\times0,8\times0,8=4,76\left(m^2\right)\)
Diện tích xung quanh và trần nhà là::
\(2\times4\times\left(8+6\right)+6\times8=160\left(m^2\right)\)
Diện tich cần quét vôi là:
\(160-4,76=155,24\left(m^2\right)\)

\(\dfrac{x-1}{2011}+\dfrac{x-2}{2010}+\dfrac{x-3}{2009}+\dfrac{x-4}{2008}=4\)
=>\(\left(\dfrac{x-1}{2011}-1\right)+\left(\dfrac{x-2}{2010}-1\right)+\left(\dfrac{x-3}{2009}-1\right)+\left(\dfrac{x-4}{2008}-1\right)=0\)
=>\(\dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}+\dfrac{x-2012}{2008}=0\)
=>\(\left(x-2012\right)\left(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}+\dfrac{1}{2008}\right)=0\)
=>x-2012=0
=>x=2012
\(\dfrac{x-1}{2011}+\dfrac{x-2}{2010}+\dfrac{x-3}{2009}+\dfrac{x-4}{2008}=4\\ \left(\dfrac{x-1}{2011}-1\right)+\left(\dfrac{x-2}{2010}-1\right)+\left(\dfrac{x-3}{2009}-1\right)+\left(\dfrac{x-4}{2008}-1\right)=0\\ \dfrac{x-2012}{2011}+\dfrac{x-2012}{2010}+\dfrac{x-2012}{2009}+\dfrac{x-2012}{2008}=0\\ \left(x-2012\right)\left(\dfrac{1}{2011}+\dfrac{1}{2010}+\dfrac{1}{2009}+\dfrac{1}{2008}\right)=0\\ x-2012=0\\ x=2012\)

Đổi: 8 phút = \(\dfrac{2}{15}\left(h\right)\)
Vận tốc của xe đạp là:
\(1,6:\dfrac{2}{15}=12\left(km/h\right)\)
1,6km=1600m
Vận tốc của xe đạp là 1600:8=200(m/p)=12km/h
=>Chọn C

1: Sửa đề: Vẽ \(\widehat{x'Ay'}\) là góc đối đỉnh của góc xAy
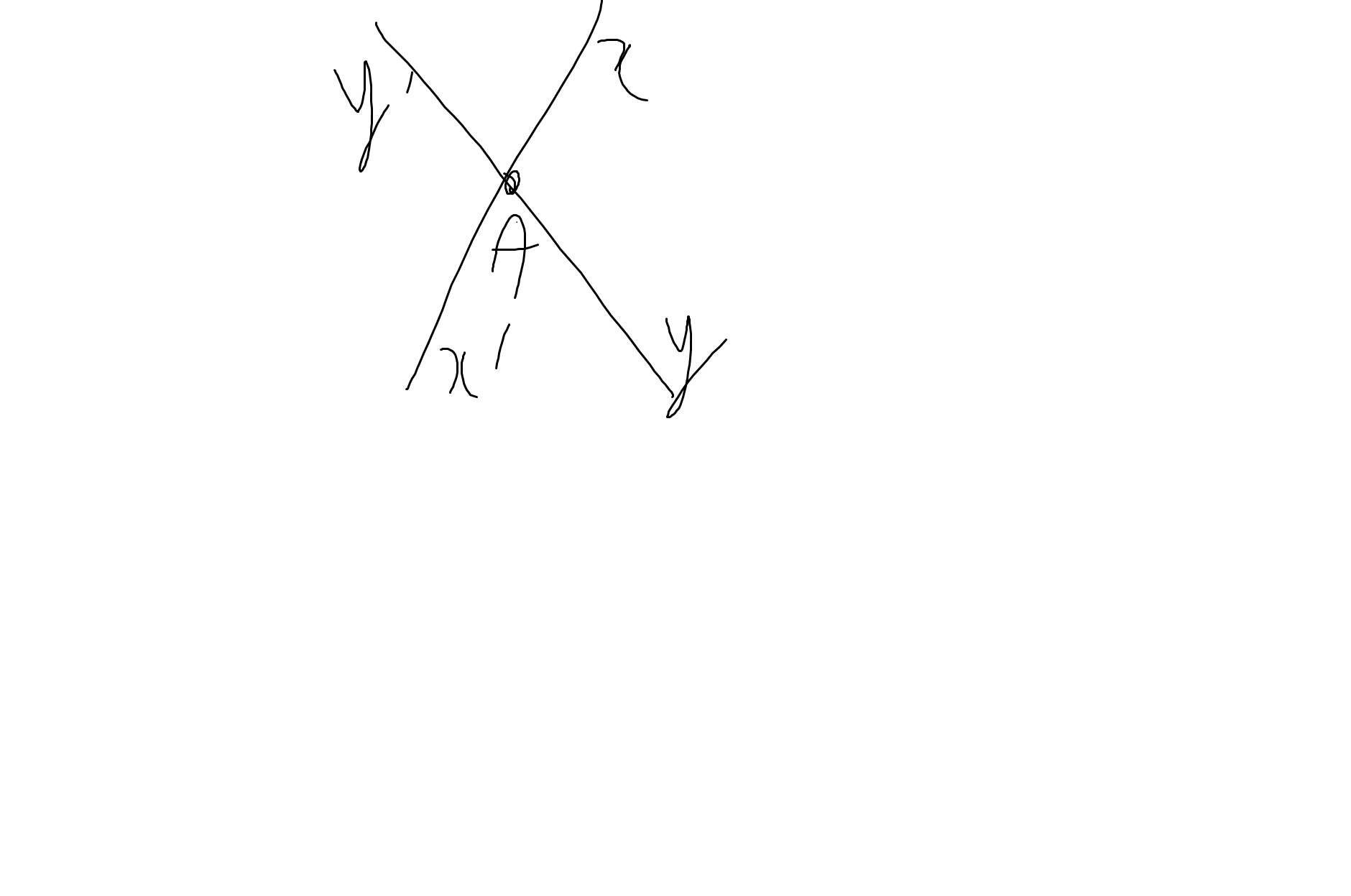
2: Ta có: \(\widehat{xAy}+\widehat{xAy'}=180^0\)(hai góc kề bù)
=>\(\widehat{xAy'}+100^0=180^0\)
=>\(\widehat{xAy'}=80^0\)
Ta có: \(\widehat{xAy}=\widehat{x'Ay'}\)(hai góc đối đỉnh)
mà \(\widehat{xAy}=100^0\)
nên \(\widehat{x'A'y}=100^0\)
Ta có: \(\widehat{xAy'}=\widehat{x'Ay}\)(hai góc đối đỉnh)
mà \(\widehat{xAy'}=80^0\)
nên \(\widehat{x'Ay}=80^0\)

\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\\ =\left(\dfrac{3}{4}\right)^{3+5}:\dfrac{3^7}{8^7}\\ =\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}\\ =\dfrac{3^8}{2^{16}}\cdot\dfrac{2^{21}}{3^7}=3\cdot2^5=3\cdot32=96\)
\(\left[\left(\dfrac{4}{3}\right)^{-3}\cdot\left(\dfrac{3}{4}\right)^5\right]:\left(\dfrac{3}{8}\right)^7\)
\(=\left[\left(\dfrac{3}{4}\right)^3\cdot\left(\dfrac{3}{4}\right)^5\right]:\dfrac{3^7}{8^7}\)
\(=\left(\dfrac{3}{4}\right)^8\cdot\dfrac{8^7}{3^7}=\dfrac{3^8}{4^8}\cdot\dfrac{8^7}{3^7}=\dfrac{3\cdot2^{21}}{2^{16}}=3\cdot2^5=3\cdot32=96\)

Hiệu của hai số khi tăng số lớn thêm 3 đơn vị và giảm số bé đi 2 đơn vị là:
35+3-(-2)=38+2=40
Số lớn khi đó là 40:4x5=50
Số lớn là 50-3=47
Số bé là 47-35=12

a: \(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\9x+3y=27\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+3y-x-3y=27-11\\x+3y=11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x=16\\3y=11-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{11-x}{3}=\dfrac{11-2}{3}=\dfrac{9}{3}=3\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+10y-3x=-1\\2x+4-3x+15y=-12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y=-1\\-x+15y=-16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\-2x+30y=-32\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+10y-2x+30y=-1+\left(-32\right)\\x-15y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}40y=-33\\x=15y+16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=15\cdot\dfrac{-33}{40}+16=\dfrac{29}{8}\end{matrix}\right.\)
a)
\(\left\{{}\begin{matrix}x+3y=11\\3x-y=9-2y\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+3y=11\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}3x+9y=33\\3x+y=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}8y=24\\3x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\3x+3=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3\\x=\dfrac{6}{3}=2\end{matrix}\right.\)
b)
\(\left\{{}\begin{matrix}5\left(x+2y\right)=3x-1\\2x+4=3\left(x-5y\right)-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x+10y=3x-1\\2x+4=3x-15y-12\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+10y=-1\\2x-30y=32\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}40y=-33\\x-15y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x+\dfrac{99}{8}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{33}{40}\\x=16-\dfrac{99}{8}=\dfrac{29}{8}\end{matrix}\right.\)
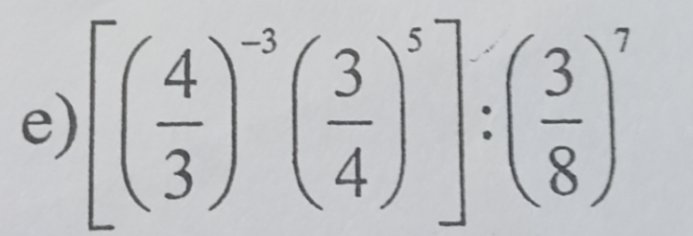
Đặt 5x+17-(2x+5)=0
=>5x+17-2x-5=0
=>3x+12=0
=>3x=-12
=>\(x=-\dfrac{12}{3}=-4\)