\(\dfrac{ }{ }\)\(\dfrac{ }{ }\)Giup cau a,d vs a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a; a - b = 6 và \(\overline{4a7}\) + \(\overline{1b5}\) ⋮ 9
Để \(\overline{4a7}\) + \(\overline{1b5}\) ⋮ 9 ⇔ 4 + a + 7 + 1 + b + 5 ⋮ 9
⇒(4 + 7 + 1 + 5) + a + b ⋮ 9
⇒ 17 + a + b ⋮ 9
⇒ 8 + a + b ⋮ 9
Vì a + b ≤ 18 ⇒ 8 + a + b ≤ 26 ⇒ 8 + a + b = 9; 18 (1)
a - b = 6 ⇒ a = 6 + b Thay a = 6 + b vào (1) ta có:
8 + 6 + b + b = 9; 18 ⇒ (8 + 6) + (b + b) = 9; 18
⇒ 14 + 2b = 9; 18
Lập bảng ta có:
| 14 + 2b | 9 | 18 |
| b | -\(\dfrac{5}{2}\) | 2 |
| a = 6 + b | 8 | |
| a; b \(\in\) N; 0 ≤ a; b ≤ 9 | loại |
Theo bẳng trên ta có (a; b) = (8; 2)
b; a - b = 6 và \(\overline{7a5}\) + \(\overline{8b4}\) ⋮ 9
\(\overline{7a5}\) + \(\overline{8b4}\) ⋮ 9 ⇔ 7 + a + 5 + 8 + b + 4 ⋮ 9 ⇒ (7 + 5 + 8 + 4) + a + b⋮ 9
⇒ (12 + 8 + 4) + a + b ⋮ 9 ⇒ (20 + 4) + a + b ⋮ 9 ⇒ 24 + a + b ⋮ 9
⇒ 6 + a + b ⋮ 9 vì 0 ≤ a + b ≤ 18 ⇒ 6 ≤ 6 + a + b ≤ 24
⇒ 6 + a + b = 9; 18 (1)
a - b = 6 ⇒ a = 6 + b thay a = b + 6 vào (1) ta có:
6 + 6 + b + b = 9; 18 ⇒ (6 + 6) + (b + b) = 9; 18 ⇒ 12 +2b = 9; 18
Lập bảng ta có:
| 12 + 2b | 9 | 18 |
| b | - \(\dfrac{3}{2}\) | 3 |
| a = 6 + 3 | 9 | |
| 0 ≤ a; b ≤ 9; a; b \(\in\) N | Loại |
Theo bảng trên ta có:
(a; b) = (9; 3)

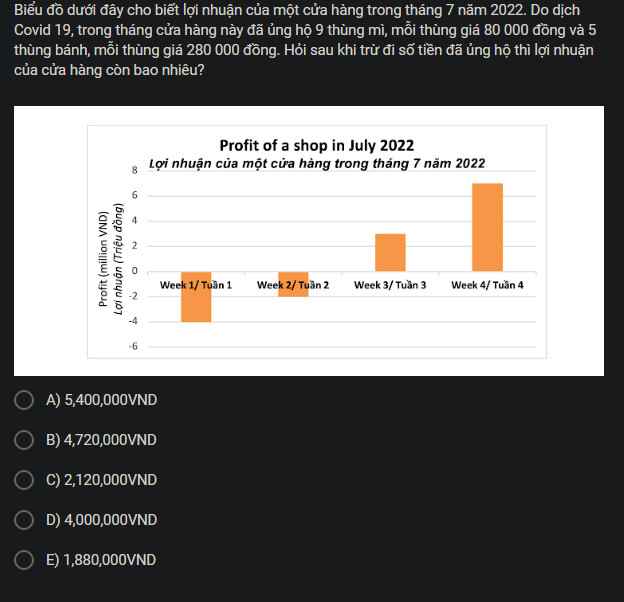
Số tiền lợi nhuận ban đầu là:
-4-2+3+7=10-6=4(triệu đồng)
Số tiền đã chi ra là:
\(9\cdot80000+5\cdot280000=2120000\left(đồng\right)=2,12\left(triệuđồng\right)\)
Số tiền còn lại là:
4-2,12=1,88(triệu đồng)
=>Chọn E

2:
\(AM=\dfrac{1}{3}\cdot AB=\dfrac{1}{3}\cdot48=16\left(cm\right)\)
\(AN=\dfrac{1}{2}\cdot AD=\dfrac{1}{2}\cdot36=18\left(cm\right)\)
ΔAMN vuông tại A
=>\(S_{AMN}=\dfrac{1}{2}\times AM\times AN=\dfrac{1}{2}\times16\times18=144\left(cm^2\right)\)
BM+AM=BA
=>BM+16=48
=>BM=32(cm)
AN+ND=AD
=>ND+18=36
=>ND=18(cm)
ΔNDC vuông tại D
=>\(S_{NDC}=\dfrac{1}{2}\times ND\times DC=\dfrac{1}{2}\times18\times48=432\left(cm^2\right)\)
ΔMBC vuông tại B
=>\(S_{MBC}=\dfrac{1}{2}\times BM\times BC=\dfrac{1}{2}\times32\times36=576\left(cm^2\right)\)
ABCD là hình chữ nhật
=>\(S_{ABCD}=AB\times AD=48\times36=1728\left(cm^2\right)\)
\(S_{ABCD}=S_{AMN}+S_{NDC}+S_{MBC}+S_{MNC}\)
=>\(S_{MNC}+144+432+576=1728\)
=>\(S_{MNC}=576\left(cm^2\right)\)

Ví dụ 3:
Giải:
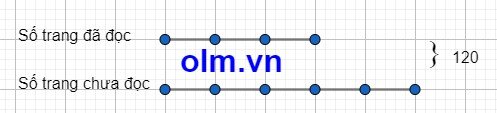
Tỉ số số trang đã đọc và số trang chưa đọc là: \(\dfrac{1}{5}:\dfrac{1}{3}=\dfrac{3}{5}\)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số trang chưa đọc là: 120: (5 + 3) x 5 = 75 (trang)
Số trang đã đọc là: 120 - 75 = 45 (trang)
Đáp số: Số trang chưa đọc là: 75 trang
Số trang đã đọc là: 45 trang

Bài 8: Giải:
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Số tiền lớp 4A quyên góp được là:
98 000 : (5 - 3) x 5 = 245 000 (đồng)
Số tiền của lớp 4B quyên góp được là:
245 000 - 98 000 = 147 000 (đồng)
Đáp số:...
Bài 10:
\(\dfrac{17}{2}\times\dfrac{3}{5}+\dfrac{3}{5}\times\dfrac{1}{2}+\dfrac{3}{5}\\=\dfrac{17}{2}\times\dfrac{3}{5}+\dfrac{1}{2}\times\dfrac{3}{5}+\dfrac{3}{5}\times1\\ =\dfrac{3}{5}\times\left(\dfrac{17}{2}+\dfrac{1}{2}+1\right)\\ =\dfrac{3}{5}\times\left(9+1\right)\\ =\dfrac{3}{5}\times10\\ =3\times2\\ =6\)

11.
a)
\(A=\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\\=\left(x+1\right)\left(x^2-x\cdot1+1^2\right)-\left(x-1\right)\left(x^2+x\cdot1+1^2\right)\\ =\left(x^3+1^3\right)-\left(x^3-1^3\right)\\ =x^3+1-x^3+1\\ =2\)
=> Giá trị của bt không phụ thuộc vào biến
b)
\(B=\left(2x+6\right)\left(4x^2-12x+36\right)-8x^3+10\\ =\left(2x+6\right)\left[\left(2x\right)^2-2x\cdot6+6^2\right]-8x^3+10\\ =\left[\left(2x\right)^3+6^3\right]-8x^3+10\\ =\left(8x^3+216\right)-8x^3+10\\ =8x^3+216-8x^3+10\\ =226\)
=> Giá trị của bt không phụ thuộc vào biến
6.
\(a)\left(x+1\right)^3=x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=x^3+3x^2+3x+1\\ b)\left(2x+3\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot3+3\cdot2x\cdot3^2+3^3=8x^3+36x^2+54x+27\\ c)\left(x^2+2\right)^3=\left(x^2\right)^3+3\cdot\left(x^2\right)^2\cdot2+3\cdot x^2\cdot2^2+2^3=x^6+6x^4+12x^2+8\\ d)\left(2x+5y\right)^3=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot5y+3\cdot2x\cdot\left(5y\right)^2+\left(5y\right)^3=8x^3+60x^2y+150xy^2+125y^3\\ e.\left(x+\dfrac{1}{2}\right)^3=x^3+3\cdot x^2\cdot\dfrac{1}{2}+3\cdot x\cdot\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3=x^3+\dfrac{3}{2}x^2+\dfrac{3}{4}x+\dfrac{1}{8}\\ g.\left(\dfrac{1}{2}x+y^2\right)=\left(\dfrac{1}{2}x\right)^3+3\cdot\left(\dfrac{1}{2}x\right)^2\cdot y^2+3\cdot\dfrac{1}{2}x\cdot\left(y^2\right)^2+\left(y^2\right)^3\\ =\dfrac{x^3}{8}+\dfrac{3}{4}x^2y^2+\dfrac{3}{2}xy^4+y^6\\ h.\left(x^2-2\right)^3=\left(x^2\right)^3-3\cdot\left(x^2\right)^2\cdot2+3\cdot x^2\cdot2^2-2^3=x^6-6x^4+12x^2-8\)

11A:
a) Thay t = 1 vào A ta có:
\(A=1^4+2\cdot1^2+2022=1+2+2022=2025\)
b) Thay m = 4 và n = 2 vào B ta có:
\(B=4^2:2^2+\left(4-2\right)^2+1=16:4+2^2+1=4+4+1=9\)
11B
a) Thay a = 3 vào C ta có:
\(C=\left(2+3\right)^2+\left(3-2\right)^{2021}=5^2+1^{2021}=25+1=26\)
b) Thay a = 4 và b = 5 vào D ta có:
\(D=4\cdot5^2-\left(4+5\right)^2-1=4\cdot25-9^2-1=100-81-1=18\)
12B:
a: Độ dài cạnh là \(\dfrac{4a}{4}=a\)(m)
Diện tích hình vuông MNPQ là; \(S=a^2\)
b: Khi a=2 thì \(S=2^2=4\left(m^2\right)\)
13A:
Ngày thứ hai bán được:
5124-480=4644(lít)
Số lít dầu bán được trong ngày thứ ba là:
\(4644\cdot2=9288\left(lít\right)\)

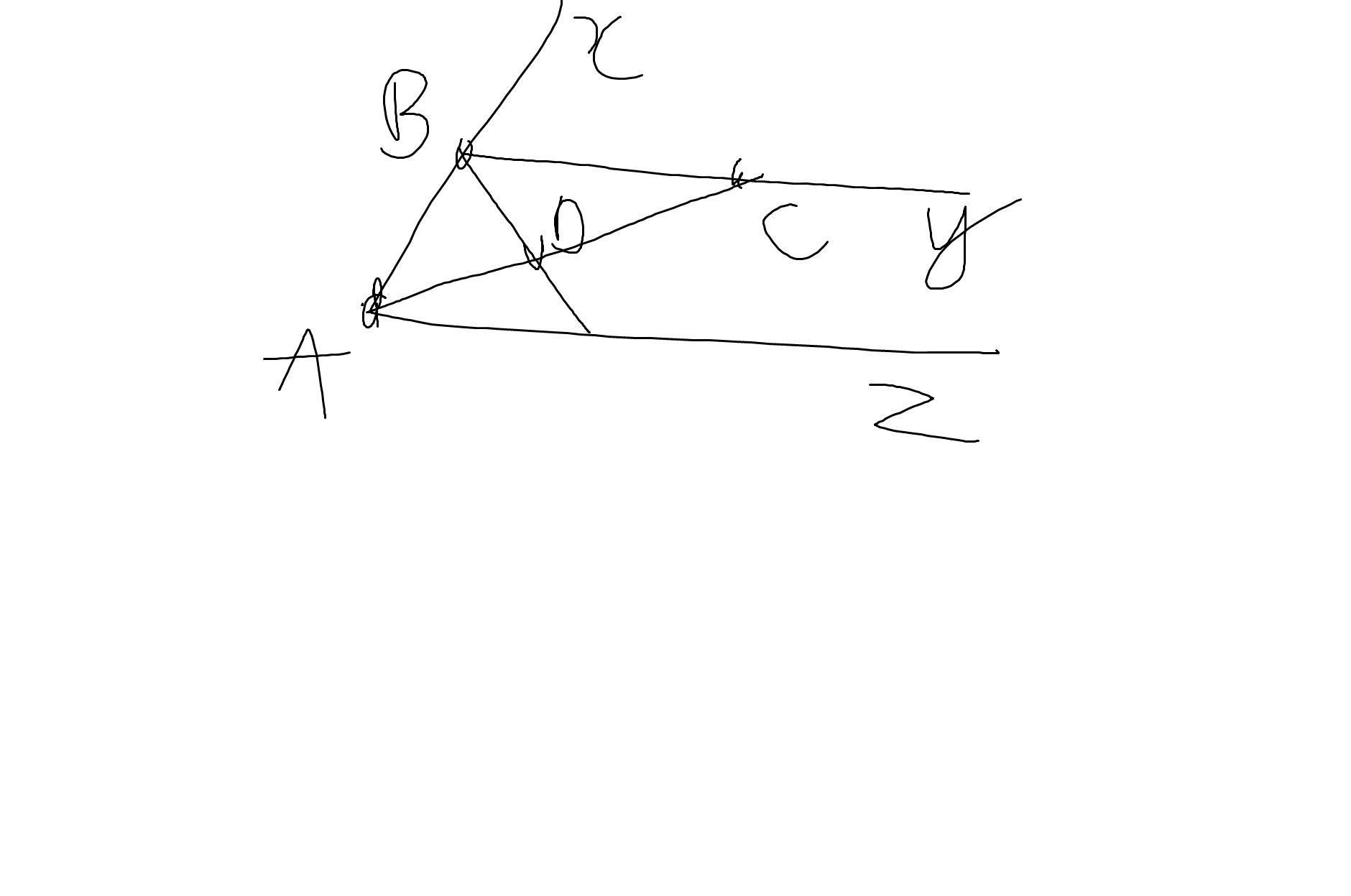
a: Ta có: \(\widehat{xBy}=\widehat{xAz}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên By//Az
b: Ta có: \(\widehat{ABC}+\widehat{xBC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABC}+60^0=180^0\)
=>\(\widehat{ABC}=120^0\)
AC là phân giác của góc zAB
=>\(\widehat{BAC}=\dfrac{\widehat{xAB}}{2}=30^0\)
Xét ΔBAC có \(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^0\)
=>\(\widehat{BCA}+120^0+30^0=180^0\)
=>\(\widehat{BCA}=30^0\)
c: Ta có: BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=60^0\)
Xét ΔDBA có \(\widehat{DBA}+\widehat{DAB}=60^0+30^0=90^0\)
nên ΔBDA vuông tại D
=>BD\(\perp\)AC

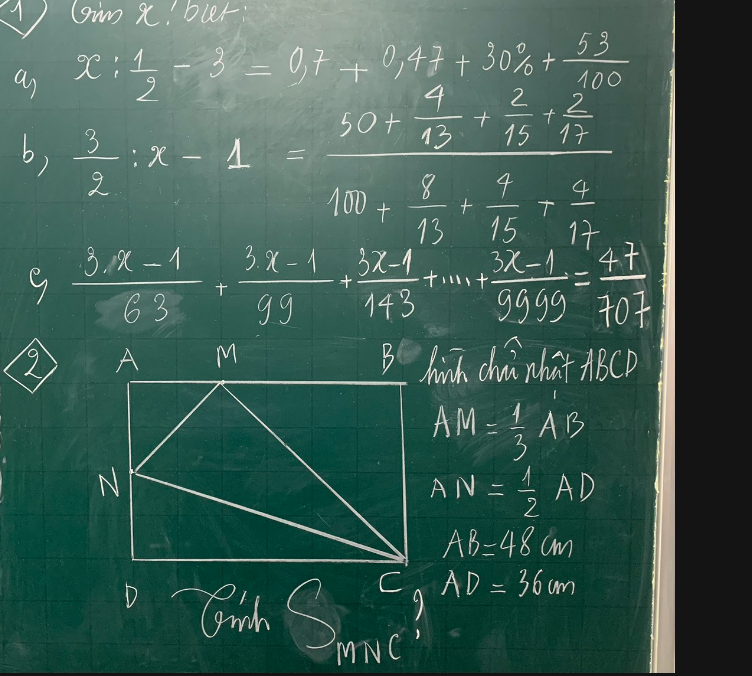


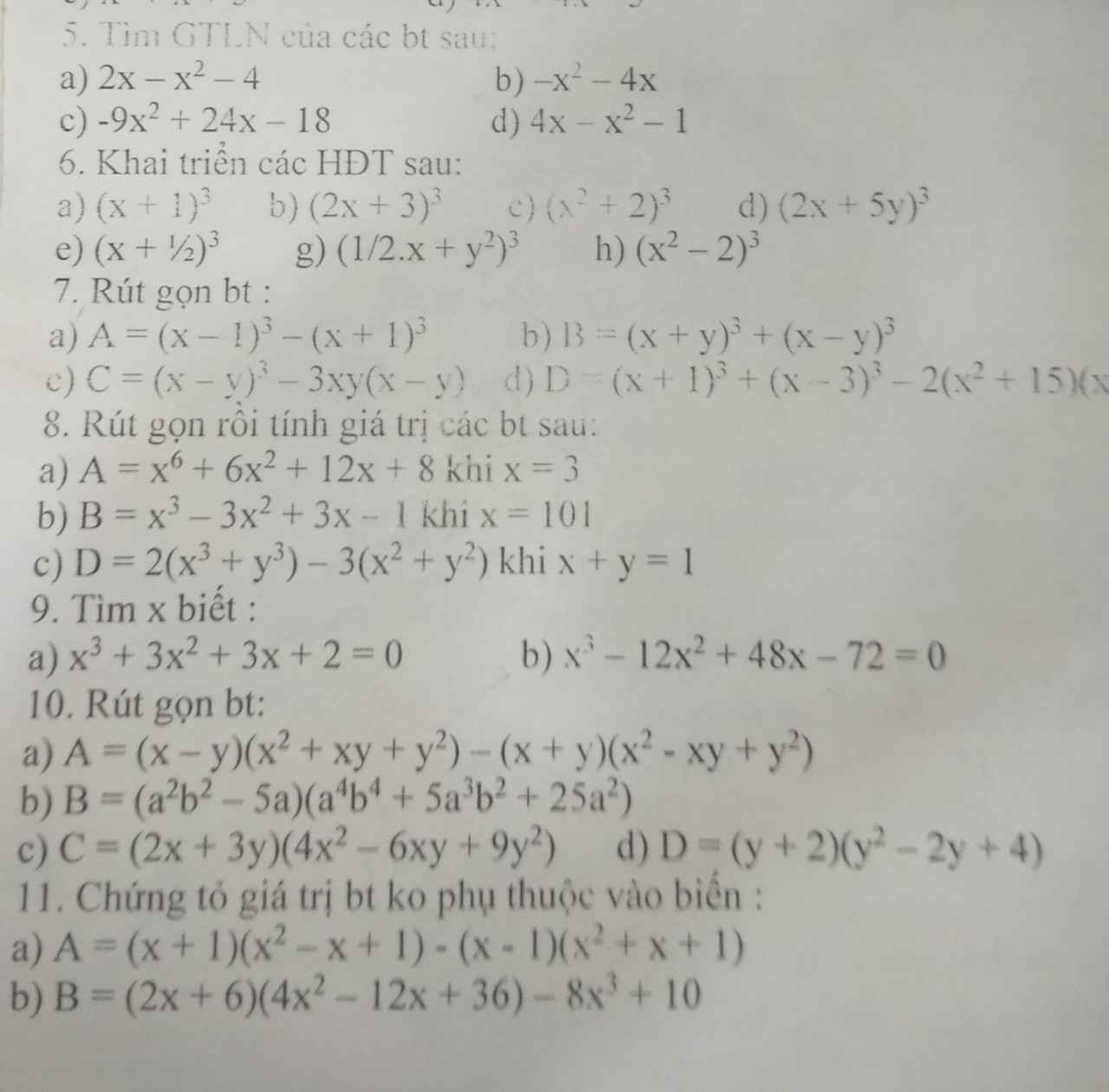


a:
d: