\(\dfrac{17}{4}-3\times\dfrac{7}{6}\\ =\dfrac{17}{4}-\dfrac{21}{6}\\ =\dfrac{51}{12}-\dfrac{42}{12}=\dfrac{9}{12}=\dfrac{3}{4}\)

thanks nha

A = \(\dfrac{8}{9}+\dfrac{24}{25}\) + \(\dfrac{48}{49}\) + ... + \(\dfrac{10200}{10201}\)

A = \(\dfrac{8}{3^2}\) + \(\dfrac{24}{5^2}\) + \(\dfrac{48}{7^2}\)  + ... + \(\dfrac{10200}{101^2}\)

Xét dãy số: 3; 5; 7;...; 101

Dãy số trên là dãy số cách đều với khoảng là: 5 - 3 = 2

Số số hạng của dãy số trên là: (101 - 3): 2 + 1 = 50

Vậy A có 50 hạng tử

     \(\dfrac{8}{9}\)  < \(1\)

     \(\dfrac{24}{25}\) < 1

    \(\dfrac{48}{49}\) < 1

  ..................

\(\dfrac{10200}{10201}\) < 1

Cộng vế với vế ta có: 

A = \(\dfrac{8}{9}\) + \(\dfrac{24}{25}\) + \(\dfrac{48}{49}\) +....+ \(\dfrac{10200}{10201}\) < 1 x 50

A < 50 < 99,75 (trái với đề bài)

Vậy việc chứng minh A > 99,75 là điều không thể xảy ra. 

\(A=\dfrac{1}{2\cdot6}+\dfrac{1}{3\cdot8}+...+\dfrac{1}{2023\cdot4048}\)

\(=\dfrac{2}{4\cdot6}+\dfrac{2}{6\cdot8}+...+\dfrac{2}{4046\cdot4048}\)

\(=\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{4046}-\dfrac{1}{4048}\)

\(=\dfrac{1}{4}-\dfrac{1}{4048}=\dfrac{1011}{4048}\)

\(A=\frac{1}{2.6}+\frac{1}{3.8}+\frac{1}{4.10}+...+\frac{1}{2023.4048}\\=\frac12\left(\frac{2}{2.6}+\frac{2}{3.8}+\frac{2}{4.10}+...+\frac{2}{2023.4048}\right)\\=\frac12\left( \frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{2023.2024}\right)\\=\frac12\left(\frac12-\frac13+\frac13-\frac14+\frac14-\frac15+...+\frac{1}{2023}-\frac{1}{2024}\right)\\=\frac12\left(\frac12-\frac{1}{2024}\right) \\=\frac12.\frac{1011}{2024}=\frac{1011}{4048}\)

\(-3\left(x^2+5\right)-\left(x+1\right)\left(3x-9\right)=3x+10\)

=>\(-3x^2-15-3x^2+9x-3x+9=3x+10\)

=>\(-6x^2+6x-6-3x-10=0\)

=>\(-6x^2+3x-16=0\)

\(\text{Δ}=3^2-4\cdot\left(-6\right)\left(-16\right)=9-4\cdot96=-375< 0\)

=>Phương trình vô nghiệm

-3(x² + 5) - (x + 1)(3x - 9) = 2x + 10

-3x² - 15 - 3x² + 9x - 3x + 9 = 2x + 10

-6x² + 6x - 6 = 2x + 10

-6x² + 6x - 6 - 2x - 10 = 0

-6x² + 4x - 16 = 0

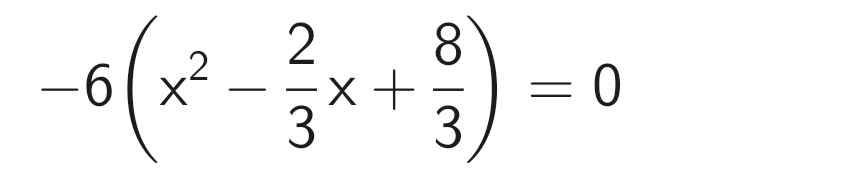  Ta có:

x² - 2/3 x + 8/3

= x² - 2.x.1/3 + (1/3)² + 23/9

= (x - 1/3)² + 23/9 > 0 với mọi x ∈ R

⇒ -6[(x - 1/3)² + 23/9] < 0 với mọi x ∈ R

Vậy không tìm được x thỏa mãn đề bài

17 × 2 555 = 43 435

43 435 × 23 = 997 805

997 805 × 119 = 118 706 495

95 × 23 = 2 185

2 185 × 12 357 = 27 003 945

27 003 945 × 69 = 1 863 247 105

118 706 495 - 1 863 247 105 = -1 744 540 610

Vậy chữ số cuối cùng của biểu thức trên là 0.

khi ta nhân 1 số lẻ với số có tận cùng là 5 thì tận cùng của chúng cũng là 5. vậy 17 x 2 555 x 23 x 119 - 95 x 23 x 12 357 x 69

=.......5 - .........5

= .....0

Biểu thức trên có tận cùng là 0

Diện tích tấm bìa ban đầu là:

\(\frac95\times\frac56=\frac32(m^2)\)

Diện tích tấm bìa Hoa đã cắt đi là:

\(\frac32\times\frac45=\frac65(m^2)\)

Diện tích tấm bìa còn lại là:

\(\frac32-\frac65=\frac{3}{10}(m^2)\)

Diện tích của tấm bìa đó là:

     \(\dfrac{9}{5}\times\dfrac{5}{6}=\dfrac{3}{2}=1,5\) ( m² )

Hoa đã cắt số mét vuông là:

     1,5 x \(\dfrac{4}{5}\) = 1,2 ( m² )

Diện tích còn lại của tấm bìa là:

     1,5 - 1,2 = 0,3 ( m² )

           Đáp số: 0,3 m²

a: Vì \(\widehat{xOy};\widehat{zOy}\) là hai góc kề nhau nên tia Oy nằm giữa hai tia Ox,Oz

=>\(\widehat{xOy}+\widehat{zOy}=\widehat{xOz}=120^0\)

mà \(\widehat{xOy}-\widehat{zOy}=40^0\)

nên \(\widehat{xOy}=\dfrac{120^0+40^0}{2}=80^0;\widehat{zOy}=80^0-40^0=40^0\)

b: Ta có: \(\widehat{xOm}+\widehat{xOy}=180^0\)(hai góc kề bù)

=>\(\widehat{xOm}+80^0=180^0\)

=>\(\widehat{xOm}=100^0\)

c: Ta có: \(\widehat{mOn}=\widehat{yOz}\)(hai góc đối đỉnh)

mà \(\widehat{yOz}=40^0\)

nên \(\widehat{mOn}=40^0\)

a) Ta có:

\(\widehat{xOy}+\widehat{zOy}=\widehat{xOz}=120^o\) (hai góc kề nhau)

Mà \(\widehat{xOy}-\widehat{zOy}=40^o\) nên:

\(\widehat{xOy}=\dfrac{120^o+40^o}{2}=80^o\)

Do đó: \(\widehat{zOy}=120^o-80^o=40^o\)

Vậy...

b) Ta có:

\(\widehat{xOy}+\widehat{xOm}=180^o\) (hai góc kề bù)

Mà \(\widehat{xOy}=80^o\) nên:

\(\widehat{xOm}=180^o-80^o=100^o\)

Vậy...

c) Ta có:

\(\widehat{mOn}=\widehat{zOy}\) (hai góc đối đỉnh)

Mà \(\widehat{zOy}=40^o\) nên:

\(\widehat{mOn}=40^o\)

Vậy...

Nửa chu vi thửa ruộng trên bản đồ là:

20:2=10(cm)

Chiều dài trên bản đồ là (10+2):2=6(cm)

Chiều rộng trên bản đồ là 6-2=4(cm)

Chiều dài thật là 6x1000=6000(cm)=60(m)

Chiều rộng thật là 4x1000=4000(cm)=40(m)

Diện tích thật là:

60x40=2400(m²)=0,24(ha)

Bạn xem lại câu A nhé dãy A toàn các số hạng chia hết cho 3 mà số cuối 2023 lại không chia hết cho 3, dãy A không tuân theo quy luật nào cả không thể tính được bạn nhé

H = 2012.3+2012.4+...+2012.2011

= 2012.(3+4+...+2011)

Xét riêng: B=3+4+...+2011

Số số hạng dãy trên:

  (2011-3):1+1=2009 (số hạng)

Tổng dãy B là:

  (2011+3).2009:2=2023063

Do vậy: H = 2012.2023063 = 4070402756

Mình nghĩ bạn chép sai phần A của câu hỏi rồi vì mỗi số hạng đều chia hết cho 3 nên xin phép sửa nhé!

\(A=3+6+9+...+2022\)

Số số hạng của biểu thức A là:

\(\left(2022-3\right):3+1=674\) (số)

\(\Rightarrow A=\left(2022+3\right)\cdot674:2\)

\(\Rightarrow A=682425\)

Vậy \(\Rightarrow A=682425\)

\(H=2012\cdot3+2012\cdot4+...+2012\cdot2011\)

\(\Rightarrow H=2012\cdot\left(3+4+...+2011\right)\)

Đặt \(B=3+4+...+2011\)

Số số hạng của biểu thức B là:

\(\left(2011-3\right):1+1=2009\) (số)

\(\Rightarrow B=\left(2011+3\right)\cdot2009:2\)

\(\Rightarrow B=2023063\)

Thay \(B=2023063\) vào H được:

\(H=2012\cdot2023063\)

\(\Rightarrow H=4070402756\)

Vậy \(H=4070402756\)