trong cuộc sống có những trải nghiệm cho chúnh ta niềm vui và hạnh phúc. Hãy kể lạichuyến trải nghiệm đến K9 cùng các bạn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{3}{1.2}+\dfrac{3}{2.3}+\dfrac{3}{3.4}+...+\dfrac{3}{2021.2022}\)
\(=3\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2021.2022}\right)\)
\(=3.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\right)\)
\(=3.\left(1-\dfrac{1}{2022}\right)\)
\(=\dfrac{2021}{674}\)

\(\left(x-2\right).\left(x-2\right)+2024=\left(x-2\right)^2+2024\ge2024\forall x\in R\\ Vậy:min_{BT}=2024\Leftrightarrow x-2=0\Leftrightarrow x=2\)

Lời giải:
$\frac{3}{1\times 3}+\frac{3}{3\times 5}+\frac{3}{5\times 7}+....+\frac{3}{57\times 59}$
$=\frac{3}{2}(\frac{3-1}{1\times 3}+\frac{5-3}{3\times 5}+\frac{7-5}{5\times 7}+....+\frac{59-57}{57\times 59})$
$=\frac{3}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{57}-\frac{1}{59})$
$=\frac{3}{2}(1-\frac{1}{59})=\frac{87}{59}$
Sửa đề: \(\dfrac{3}{1.3}+\dfrac{3}{3.5}+...+\dfrac{3}{57.59}\)
\(=\dfrac{3}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{57.59}\right)\)
\(=\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{57}-\dfrac{1}{59}\right)\)
\(=\dfrac{3}{2}.\left(1-\dfrac{1}{59}\right)\)
\(=\dfrac{3}{2}.\dfrac{58}{59}=\dfrac{87}{59}\)

Suy nghĩ về công lao của cha mẹ, tôi hiểu rằng họ là những người hiến dâng tất cả cho con cái với tình thương vô bờ. Cha mẹ là những người vất vả làm việc, hy sinh và kiên nhẫn dạy dỗ, để cho con có cuộc sống tốt đẹp hơn. Thương cha nhớ mẹ không chỉ là sự nhớ nhung về hình ảnh của họ, mà còn là việc gìn giữ và trân trọng những giá trị mà họ đã truyền đạt cho chúng ta. Sự hiện diện và tình thương của cha mẹ là nguồn động viên lớn lao trong cuộc sống, là nền tảng vững chắc để chúng ta vươn lên và thành công. Mỗi khi thương cha nhớ mẹ, tôi cảm nhận được lòng biết ơn sâu sắc và quyết tâm sống đáng giá để trả công cho họ.

Lời giải:
Đặt $A=\frac{1}{20.23}+\frac{1}{23.26}+\frac{1}{26.29}+...+\frac{1}{77.80}$
$3A=\frac{3}{20.23}+\frac{3}{23.26}+\frac{3}{26.29}+...+\frac{3}{77.80}$
$=\frac{23-20}{20.23}+\frac{26-23}{23.26}+\frac{29-26}{26.29}+...+\frac{80-77}{77.80}$
$=\frac{1}{20}-\frac{1}{23}+\frac{1}{23}-\frac{1}{26}+\frac{1}{26}-\frac{1}{29}+...+\frac{1}{77}-\frac{1}{80}$
$=\frac{1}{20}-\frac{1}{80}$
$A=\frac{1}{3}(\frac{1}{20}-\frac{1}{80})=\frac{1}{60}-\frac{1}{240}< \frac{1}{60}< \frac{1}{9}$
Ta có:
\(\dfrac{1}{20.23}+\dfrac{1}{23.26}+...+\dfrac{1}{77.80}\)
\(=\dfrac{1}{3}\left(\dfrac{3}{20.23}+\dfrac{3}{23.26}+...+\dfrac{3}{77.80}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{20}-\dfrac{1}{23}+\dfrac{1}{23}-\dfrac{1}{26}+...+\dfrac{1}{77}-\dfrac{1}{80}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{20}-\dfrac{1}{80}\right)\)
\(=\dfrac{1}{3}.\dfrac{3}{80}=\dfrac{1}{80}< \dfrac{1}{9}\) (đpcm)

A = 5 + 52 + 53 + ... + 5100
5A = 52 + 53 + 54 + ... + 5101
5A - A = (52 + 53 + 54 + ... + 5101) - (52 + 53 + 54 + ... + 5100)
4A = 52 + 53 + 54 + ... + 5101 - 52 - 53 - 54 - ... - 5100
4A = (52 - 52) + (53 - 53) + (54 - 54) + ... + (5100 - 5100) + (5101 - 5)
4A = 0 + 0 + ... 0 + 5101 - 5
A = \(\dfrac{5^{101}-5}{4}\)
b; 4.A + 5 = 5n
5101 - 5 + 5 = 5n
5101 = 5n
n = 101
Vậy n = 101

Lời giải:
a. Sau 1 năm Trúc nhận được số tiền cả vốn lẫn lãi là:
$10000000+10000000\times 6:100=10600000$ (đồng)
b. Nếu bạn chỉ gửi tiền với lãi suất không kỳ hạn thì sau 40 ngày bạn nhận tổng cộng:
$10000000+10000000\times \frac{0,3}{100}\times \frac{40}{365}=10003287$ (đồng)
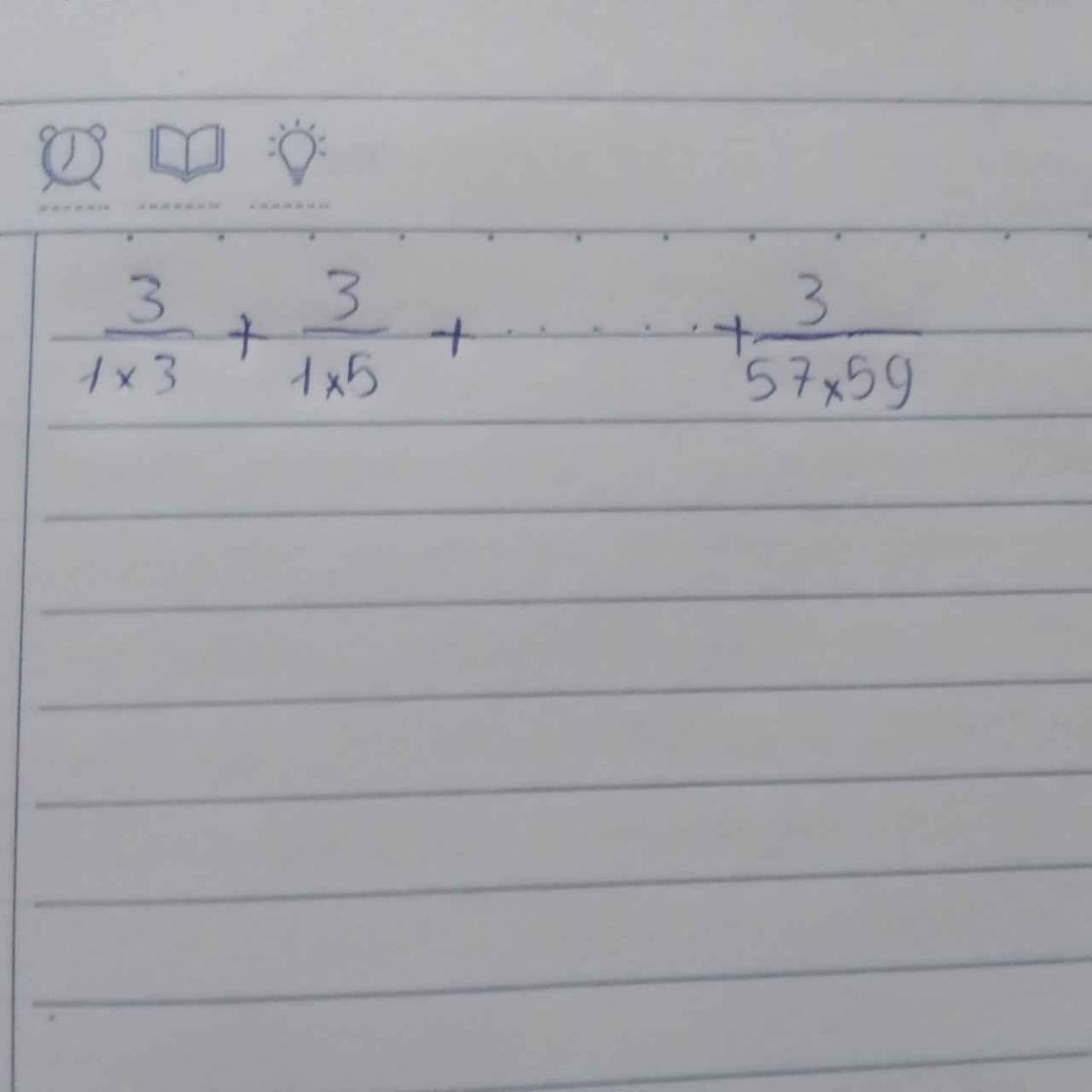

Dù là con người hay là K9, việc trải nghiệm những cuộc phiêu lưu và chia sẻ niềm vui với bạn bè luôn là một trải nghiệm đáng nhớ. Hãy cùng tưởng tượng một cuộc hành trình đến K9 cùng các bạn:
Một ngày nắng đẹp, tôi quyết định tổ chức một chuyến đi dã ngoại đến K9 cùng với nhóm bạn của mình và những chú chó cưng đáng yêu. Chúng tôi chuẩn bị đủ mọi thứ: thức ăn, nước uống, đồ dùng cá nhân, và cả đồ chơi cho các chú cún.
Khi đến K9, chúng tôi ngạc nhiên với vẻ đẹp của cảnh quan tự nhiên. Đây là một nơi yên bình, có nhiều cây cỏ xanh mướt và con đường rộng lớn dành cho việc đi dạo. Các chú cún cũng không kém phần phấn khích, chúng nhảy nhót và chạy nhảy khắp nơi.
Chúng tôi bắt đầu một cuộc trò chuyện vui vẻ và chia sẻ những kỷ niệm của mỗi người với những chú cún của mình. Các chú cún cũng tham gia vào cuộc trò chuyện bằng cách vẫy đuôi và sủa vui vẻ, như thể chúng cũng muốn chia sẻ những trải nghiệm của mình.
Chúng tôi quyết định dừng lại để nghỉ ngơi và ăn trưa. Chúng tôi dựng lều, sắp xếp đồ ăn và cùng nhau thưởng thức bữa trưa ngon lành dưới nắng vàng ấm áp. Các chú cún cũng tham gia vào bữa ăn của mình với đồ ăn ngon lành được chuẩn bị đặc biệt cho chúng.
Sau khi đã no và đầy năng lượng, chúng tôi tiếp tục cuộc hành trình của mình, khám phá những nơi mới, chơi đùa với các chú cún và tận hưởng những khoảnh khắc đáng nhớ. Khi mặt trời bắt đầu lặn và buổi tối đang đến gần, chúng tôi quyết định trở về nhà với những kỷ niệm đẹp và niềm vui không thể nào quên được.
Cuộc hành trình đến K9 cùng các bạn và các chú cún không chỉ là một trải nghiệm tuyệt vời với thiên nhiên và bạn bè, mà còn là một cơ hội để tận hưởng niềm vui và hạnh phúc của cuộc sống.