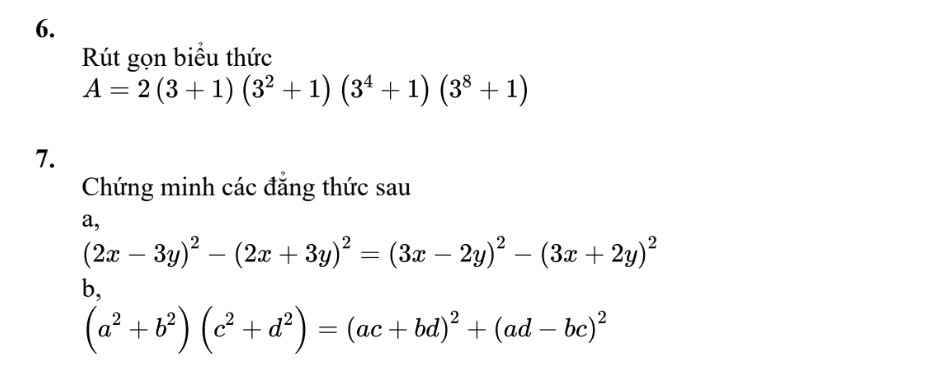
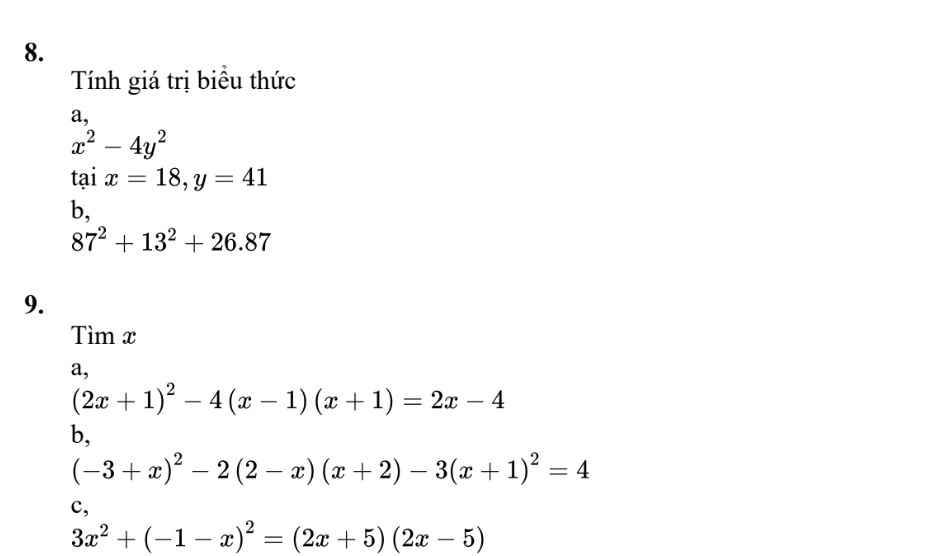
giúp mk bài 7,8,9 vs mn =,< (mk cảm ơn trước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(C=\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}\)
\(C=\dfrac{abc}{a^3}+\dfrac{abc}{b^3}+\dfrac{abc}{c^3}\)
\(C=abc\left(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\right)\)
Vì: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=-\dfrac{1}{c}\)
\(\Rightarrow\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^3=\left(-\dfrac{1}{c}\right)^3\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{3}{ab}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=-\dfrac{1}{c^3}\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}+\dfrac{3}{ab}\left(-\dfrac{1}{c}\right)=0\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}+-\dfrac{3}{abc}=0\)
\(\Rightarrow\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\left(1\right)\)
Thay (1) vào C ta được:
\(C=abc\left(\dfrac{3}{abc}\right)\)
\(\Rightarrow C=3\)

a) \(\left(-x-4\right)^2\)
\(=\left(-x\right)^2-2\cdot\left(-x\right)\cdot4+4^2\)
\(=x^2+8x+16\)
b) \(\left(-5+3x\right)^2\)
\(=\left(-5\right)^2+2\cdot\left(-5\right)\cdot3x+\left(3x\right)^2\)
\(=25-30x+9x^2\)
c) \(\left(-x-3\right)\left(x-3\right)\)
\(=-\left(x+3\right)\left(x-3\right)\)
\(=-\left(x^2-9\right)\)

a, 5\(xy\) - \(\sqrt{5y}\) ( y≥0)
= \(\sqrt{5y}\).(\(x\)\(\sqrt{5y}\) - 1)
b, 4\(x^2\) - 5
= (2\(x\))2 - (\(\sqrt{5}\) )2
= (2\(x\) - \(\sqrt{5}\))(2\(x\) + \(\sqrt{5}\))

Gọi s là độ dài nửa quãng đường. Ta có thời gian đi nửa quãng đường đầu là:
\(t_1=\dfrac{s}{v_1}\)
Gọi thời gian ô tô đi nửa phần còn lại là \(t_2\) và \(t_3\) và \(t_2=t_3\)
Thời gian ô tô đi được trong mỗi đoạn này là:
\(s_2=v_2t_2\)
\(s_3=v_3t_3\)
Mà: \(t_2=t_3=\dfrac{s}{v_2+v_3}\)
Vận tốc \(v_3\) là:
\(v_{tb}=\dfrac{2v_1\left(v_2+v_3\right)}{v_2+v_3+2v_1}\) hay \(40=\dfrac{2\cdot30\cdot\left(45+v_3\right)}{45+v_3+2\cdot30}\)
\(\Leftrightarrow40=\dfrac{60\left(45+v_3\right)}{105+v_3}\)
\(\Leftrightarrow40\left(105+v_3\right)=60\left(45+v_3\right)\)
\(\Leftrightarrow2\left(105+v_3\right)=3\left(45+v_3\right)\)
\(\Leftrightarrow210+2v_3=135+3v_3\)
\(\Leftrightarrow3v_3-2v_3=210-135\)
\(\Leftrightarrow v_3=75\left(km/h\right)\)

`@` `\text {Ans}`
`\downarrow`
`(2x-3) (x+1) - 2x (2-x) - 4x^2 + 5x`
`= 2x(x+1) - 3(x+1) - 4x + 2x^2 - 4x^2 + 5x`
`= 2x^2 + 2x - 3x - 3 - 4x + 2x^2 - 4x^2 + 5x`
`= -3`
Bổ sung thêm \(1\) bước để cậu dễ hình dung ra cách thu gọn (bước tiếp theo cho dòng thứ 3):
\(=\left(2x^2+2x^2-4x^2\right)+\left(2x-3x-4x+5x\right)-3\)
\(=0+0-3=-3\)

a) Nhiệt độ ở Trái Đất nóng dần lên làm băng ở hai cực tan dần: Đây là một quá trình biến đổi vật lí, gọi là quá trình nhiệt.
b) Hiện tượng cháy rừng gây ô nhiễm môi trường: Đây là một quá trình biến đổi hóa học, vì trong quá trình cháy, chất khí và các chất hữu cơ trong cây cối bị oxi trong không khí oxy hóa, tạo ra các sản phẩm mới và giải phóng nhiệt.
c) Để làm giảm độ chua của đất trồng cần phải bón vôi: Đây là một quá trình biến đổi hóa học, vì việc bón vôi sẽ tác động hóa học lên thành phần đất, làm thay đổi độ pH và tính chất hoá học của đất.
d) Để làm giảm độ mặn của đất, phải đưa nước vào ruộng để rửa mặn: Đây cũng là một quá trình biến đổi vật lí, gọi là quá trình rửa mặn, trong đó việc đưa nước vào ruộng giúp loại bỏ muối mặn có trong đất bằng cách pha loãng và rửa trôi chúng.
e) Dây tóc bóng đèn nóng và sáng lên khi có dòng điện đi qua: Đây là một quá trình biến đổi vật lí, gọi là hiệu ứng đèn phát quang, trong đó dòng điện đi qua dây tóc bóng đèn gây tạo ra nhiệt và làm cho dây tóc bóng đèn phát quang.
f) Ethanol để lâu trong không khí có mùi chua: Đây là một quá trình biến đổi hóa học, vì trong không khí, ethanol có thể phản ứng với oxi và tạo thành axit axetic, làm thay đổi tính chất và mùi của ethanol.

Ta có BDT luôn đúng \(\left(a-b\right)^2\ge0\) \(\Leftrightarrow a^2+b^2\ge2ab\) \(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\). Do \(a^2+b^2\le2\) nên \(2\left(a^2+b^2\right)\le4\).
Do đó \(\left(a+b\right)^2\le4\) \(\Leftrightarrow-2\le a+b\le2\), suy ra đpcm. ĐTXR \(\Leftrightarrow a=b=1\)

Kí hiệu A, B, C lần lượt là tập hợp các viên sỏi trong cùng một đống sỏi và \(f\left(A\right),f\left(B\right),f\left(C\right)\) lần lượt là số dư của số viên sỏi trong đống đó khi chia cho 3. Khi đó \(f\left(A\right)=1;f\left(B\right)=2;f\left(C\right)=0\)
Nghĩa là \(f\left(A\right),f\left(B\right),f\left(C\right)\) đôi một khác nhau. Ta sẽ xét trường hợp tổng quát, là số sỏi trong mỗi đống thỏa mãn \(f\left(A\right),f\left(B\right),f\left(C\right)\) đôi một khác nhau (chứ không chỉ riêng TH 10, 11, 12). Giả sử \(f\left(A\right)=1;f\left(B\right)=2;f\left(C\right)=0\). Có tất cả 3 trường hợp xảy ra của phép biến đổi:
TH1: Lấy 2 viên sỏi, mỗi viên từ đống A và B, sau đó thêm vào đống C viên. Khi đó sau phép biến đổi, \(f\left(A\right)=0,f\left(B\right)=1,f\left(C\right)=2\).
TH2: Lấy 2 viên sỏi, mỗi viên từ đống B và C, sau đó thêm vào đống A. Khi đó sau phép biến đổi thì \(f\left(A\right)=0;f\left(B\right)=1;f\left(C\right)=2\)
TH3: Lấy 2 viên sỏi, mỗi viên từ đống A và C, sau đó thêm vào đống B. Khi đó sau phép biến đổi thì \(f\left(A\right)=0;f\left(B\right)=1;f\left(C\right)=2\)
Như vậy, từ vị trí ban đầu, cho dù ta thực hiện phép biến đổi như thế nào thì \(f\left(A\right),f\left(B\right),f\left(C\right)\) vẫn luôn đôi một khác nhau. Chính vì vậy, không thể xảy ra trường hợp 3 đống sỏi có số sỏi bằng nhau vì khi đó \(f\left(A\right)=f\left(B\right)=f\left(C\right)\)

\(\dfrac{4x-5}{x-1}=2+\dfrac{x}{x-1}\) \(\left(dkxd:x\ne1\right)\)
\(\Leftrightarrow\dfrac{4x-5}{x-1}-2-\dfrac{x}{x-1}=0\)
\(\Leftrightarrow\dfrac{4x-5-2\left(x-1\right)-x}{x-1}=0\)
\(\Leftrightarrow4x-5-2x+2-x=0\)
\(\Leftrightarrow x=3\left(tmdk\right)\)
Vậy \(S=\left\{3\right\}\)
`@` `\text {Ans}`
`\downarrow`
`8,`
`a,`
Thay \(x=18;y=41\) vào bt
\(18^2-4\cdot41^2\)
`= 18^2 - (2*41)^2`
`= 18^2 - 82^2`
`= -6400`
`b,`
\(87^2+13^2+26\cdot87\)
`= 87*(87+26) + 169`
`= 87*113 + 169`
`= 9831 + 169`
`= 10000`
\(9,\) \(a,\left(2x+1\right)^2-4\left(x-1\right)\left(x+1\right)=2x-4\)
\(\Leftrightarrow4x^2+4x+1-4\left(x^2-1\right)-2x+4=0\)
\(\Leftrightarrow4x^2+4x+1-4x^2+4-2x+4=0\)
\(\Leftrightarrow\left(4x^2-4x^2\right)+\left(4x-2x\right)+\left(1+4+4\right)=0\)
\(\Leftrightarrow2x=-9\)
\(\Leftrightarrow x=-\dfrac{9}{2}\)
Vậy \(S=\left\{-\dfrac{9}{2}\right\}\)
\(b,\left(-3+x\right)^2-2\left(2-x\right)\left(x+2\right)-3\left(x+1\right)^2=4\)
\(\Leftrightarrow9-6x+x^2-2\left(2x+4-x^2-2x\right)-3\left(x^2+2x+1\right)-4=0\)
\(\Leftrightarrow9-6x+x^2-4x-8+2x^2+4x-3x^2-6x-3-4=0\)
\(\Leftrightarrow-12x=6\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)
\(c,3x^2+\left(-1-x\right)^2=\left(2x+5\right)\left(2x-5\right)\)
\(\Leftrightarrow3x^2+1+2x+x^2=4x^2-25\)
\(\Leftrightarrow2x=-26\)
\(\Leftrightarrow x=-13\)
Vậy \(S=\left\{-13\right\}\)