a) Độ dài đường cao \(h\):

\(SinB=\dfrac{h}{AB}\Rightarrow h=AB.sin60^o=\dfrac{a\sqrt[]{2}}{2}\left(cm\right)\)

b) Nửa chu vi tam giác đó :

\(p=\dfrac{a+a+a}{2}=\dfrac{3a}{2}\)

Diện tích tam giác :

\(S=\sqrt[]{p\left(p-a\right)\left(p-a\right)\left(p-a\right)}\)

\(\Rightarrow S=\sqrt[]{p\left(p-a\right)^3}\)

\(\Rightarrow S=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{3a}{2}-a\right)^3}=\sqrt[]{\dfrac{3a}{2}\left(\dfrac{a}{2}\right)^3}=\sqrt[]{\dfrac{3a^4}{16}}=\dfrac{a^2\sqrt[]{3}}{4}\)

a:Gọi tam giác đề bài cho là ΔABC đều có AH là đường cao

=>H là trung điểm của BC

=>HB=HC=a/2

AH=căn AB^2-AH^2

=a*căn 3/2

b: S ABC=1/2*AH*BC

=a^2*căn 3/4

nói ngắn gọn luôn nhé, nó là con vật

chắc chắn đúng luôn

Cảm ơn em câu hỏi của em thật là thù vị. Về thắc mắc của em cô nghĩ chắc cũng có nhiều bạn đang muốn biết lắm ý nhỉ? Về vấn đề em hỏi cô xin trả lời như sau:

 Tình theo a ở đây không phải là a mà mình tùy chọn em nhá. a ở đây là một ẩn a, em cứ tính độ dài của tam giác đó theo ẩn a thôi em ạ!

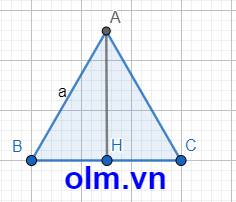
Vì ABC là tam giác đều nên đường cao cũng là đường trung tuyến của tam giác. Gọi AH là đường cao của tam giác thì

                       BH = HC =  \(\dfrac{1}{2}\)a

Xét tam giác ACH vuông tại H. Theo pytago ta có:

                AC² = AH² + HC²

               ⇒ AH² = AC² - HC²

               ⇒AH² = a² - (\(\dfrac{1}{2}\)a)² = \(\dfrac{3}{4}\)a²

              ⇒ AH = \(\sqrt{\dfrac{3}{4}a^2}\) = \(\dfrac{3\sqrt{a}}{2}\) 

\(\left(x^2+2\right).\left(x^2-3\right)\text{=}0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+2\text{=}0\\x^2-3\text{=}0\end{matrix}\right.\)

\(TH1:x^2+2\text{=}0\)

Ta thấy : \(x^2\ge0\Rightarrow x^2+2\ge2>0\)

\(\Rightarrow ptvôN_o\)

\(TH2:x^2-3\text{=}0\)

\(\Leftrightarrow x^2\text{=}3\)

\(\Leftrightarrow\left[{}\begin{matrix}x\text{=}\sqrt{3}\\x\text{=}-\sqrt{3}\end{matrix}\right.\)

Vậy.........

cần gấp!!!

\(9x^2-12xy+4y^2=\left(3x-2y\right)^2\)

\(9x^2-12xy+4y^2=\left(3x-2y\right)^2\)

Cảm ơn em đã chia sẻ bài viết rất hay và bổ ích

Cảm ơn bạn đã chia sẽ bài viết nhé. Mình sẽ áp dụng rất nhiều đó!

\(\left(x-3\right)\left(x-5\right)-\left(x-4\right)^2\)

\(=x^2-5x-3x+15-\left(x^2-8x+16\right)\)

\(=x^2-5x-3x+15-x^2+8x-16\)

\(=x^2-x^2-8x+8x+15-16=-1\)

(x - 3)(x - 5) - (x - 4)²

= x² - 5x - 3x + 15 - x² + 8x - 16

= (x² - x²) + (-5x - 3x + 8x) + (15 - 16)

= -1

Bài viết khá hay và thú vị và bổ ích anh chúc em năm lớp 8 gặp nhiều thành công trong học tập và gia đình nhé nhưng người như em thì thành công chắc chắn sẽ đến thôi 

(* Anh tặng em 5 coin nhé *)  

Vậy thất bại có vai trò gì trong cuộc sống của chúng ta không?

Thất bại có vai trò quan trọng trong cuộc sống của chúng ta. Nó không chỉ là một phần tự nhiên của quá trình thành công, mà còn là một cơ hội để học hỏi, phát triển và trưởng thành. Thất bại giúp chúng ta nhận ra những điểm yếu của mình, khám phá những cách tiếp cận mới và đạt được sự cải thiện. Nó cũng giúp chúng ta trở nên kiên nhẫn, kiên trì và đối mặt với khó khăn. Quan trọng là chúng ta hãy học cách đối diện và vượt qua thất bại để tiến bước trên con đường thành công.

Liệu nếu chúng ta gặp phải thất bại thì chúng ta nên làm gì?

Khi gặp phải thất bại, chúng ta nên không nản lòng và tiếp tục cố gắng. Đầu tiên, hãy tự đánh giá lại và tìm hiểu nguyên nhân của thất bại. Sau đó, hãy học từ kinh nghiệm đó và điều chỉnh phương pháp  của mình.  Hãy lắng nghe ý kiến và gợi ý từ những người xung quanh,  hãy tìm kiếm sự giúp đỡ từ người khác, hãy kiên nhẫn và không bỏ cuộc. Thất bại là một phần tự nhiên của cuộc sống, và chúng ta cần học cách vượt qua nó để đạt được thành công.

a, (\(x\) + y).(\(x\) + y)² - 3\(xy\).(\(x\) + y) 

= (\(x+y\))³ - 3\(x^2\)y - 3\(xy^2\)

= \(x^3\) + 3\(x^2\).y + 3\(xy^2\) + y³ - 3\(x^2\).y  - 3\(xy^2\)

= \(x^3\) + y³ 

b, (\(x-y\)).(\(x-y\))² - 3\(xy\).(\(x-y\)) 

=    (\(x\) - y)³ - 3\(x^2\).y + 3\(xy^2\)

= \(x^3\) - 3\(x^2\)y + 3\(xy^2\) - y³ - 3\(x^2\)y + 3\(xy^2\)

= \(x^3\) - 6\(x^2\)y + 6\(xy^2\) - y³

Ta có:

\(2n^3+3n^2+n=n\left(2n^2+3n+1\right)\)

\(=n\left(2n^2+2n+n+1\right)\)

\(=n\left[2n\left(n+1\right)+\left(n+1\right)\right]\)

\(=n\left(n+1\right)\left(2n+1\right)\)

\(=n\left(n+1\right)\left(2n-2+3\right)\)

\(=2\left(n-1\right)n\left(n+1\right)+3n\left(n+1\right)\)

Ta có \(n-1\) ; \(n\) và \(n+1\) là \(3\) số nguyên liên tiếp

\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮2\) và \(3\)

Do đó \(\left(n-1\right)n\left(n+1\right)⋮2.3=6\)

\(\Leftrightarrow2\left(n-1\right)n\left(n+1\right)⋮6\left(1\right)\)

Ta lại có: \(n\) và \(n+1\) là 2 số nguyên liên tiếp \(\Rightarrow n\left(n+1\right)⋮2\)

Do đó: \(3n\left(n+1\right)⋮3\)

\(\Leftrightarrow3n\left(n+1\right)⋮2.3=6\left(2\right)\)

Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra \(2n^3+3n^2+n⋮6\)

\(2n^3-3n^2+n\left(\forall n\inℤ\right)\)

\(=n\left(2n^2-3n+1\right)\)

\(=n\left(2n^2-2n-n+1\right)\)

\(=n\left[2n\left(n-1\right)-\left(n-1\right)\right]\)

\(=n\left(n-1\right)\left(2n-1\right)\)

\(=n\left(n-1\right)\left(2n+2-3\right)\)

\(=n\left(n-1\right)\left(2n+2\right)-3n\left(n-1\right)\)

\(=2n\left(n-1\right)\left(n+1\right)-3n\left(n-1\right)\) 

Ta có :

\(n\left(n-1\right)\left(n+1\right)⋮3\) (tích 3 số liên tiếp)

\(\Rightarrow2n\left(n-1\right)\left(n+1\right)⋮6\left(\forall n\inℤ\right)\left(1\right)\)

Ta lại có :

\(n\left(n-1\right)⋮2\) (tích 2 số liên tiếp là số chẵn)

\(\Rightarrow3n\left(n-1\right)⋮6\left(\forall n\inℤ\right)\left(2\right)\)

\(\left(1\right);\left(2\right)\Rightarrow2n\left(n-1\right)\left(n+1\right)-3n\left(n-1\right)⋮6\left(\forall n\inℤ\right)\)

\(\Rightarrow2n^3-3n^2+n⋮6\left(\forall n\inℤ\right)\)