Ta có: 

\(1+2+...+n=\dfrac{n\left(n+1\right)}{2}\)

\(\Rightarrow\dfrac{1}{1+2+...+n}=\dfrac{2}{n\left(n+1\right)}\)

\(\Rightarrow1-\dfrac{1}{1+2+...+n}=1-\dfrac{2}{n\left(n+1\right)}=\dfrac{n\left(n+1\right)-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)

Áp dụng:

\(\left(1-\dfrac{1}{1+2}\right)\left(1-\dfrac{1}{1+2+3}\right)...\left(1-\dfrac{1}{1+2+...+2006}\right)\)

\(=\dfrac{\left(2-1\right)\left(2+2\right)}{2.\left(2+1\right)}.\dfrac{\left(3-1\right)\left(3+2\right)}{3\left(3+1\right)}...\dfrac{\left(2006-1\right)\left(2006+2\right)}{2006.\left(2006+1\right)}\)

\(=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}...\dfrac{2005.2008}{2006.2007}\)

\(=\dfrac{1.2...2005}{2.3...2006}.\dfrac{4.5...2008}{3.4...2007}=\dfrac{1}{2006}.\dfrac{2008}{3}\)

\(=\dfrac{1004}{3009}\)

B là đáp án đúng, 14 hình

Cô ơi cô có thể giải thích giúp em được không cô

Đây là toán nâng cao hai hiệu số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau: 

                      Giải:

Hiệu số cà rốt mỗi con thỏ trong hai cách chia là: 4 - 3 = 1 (củ)

Hiệu số cà rốt trong hai cách chia là: 8 - 2 = 6 (củ)

Số thỏ là: 6 : 1 = 6 (con)

Số cà rốt là: 3 x 6 + 8 = 26 (củ)

Đáp số: thỏ 6 con, cà rốt có 26 củ

Giải:

Số kẹo Hà cho bạn lần đầu là: 40 x \(\dfrac{1}{5}\) = 8 (cái)

Tổng số kẹo Hà cho bạn là: 8 +  2 = 10 (cái)

Số kẹo Hà còn lại sau khi cho bạn là: 40 - 10 = 30 (cái)

Đáp số: 30 cái

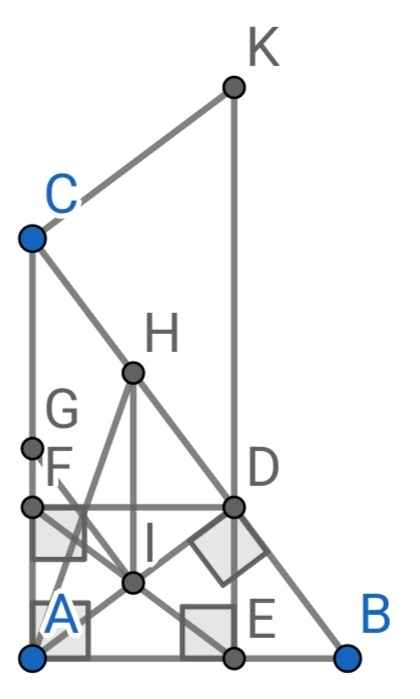
a) ∆ABC vuông tại A (gt)

⇒ AB ⊥ AC

⇒ ∠CAB = 90⁰

⇒ ∠EAF = 90⁰

Do E, F là hình chiếu của D lên AB, AC (gt)

⇒ ∠AED = ∠AFD = 90⁰

Tứ giác AEDF có:

∠EAF = ∠AED = ∠AFD = 90⁰ 

⇒ AEDF là hình chữ nhật

b) Do I là giao điểm của EF và AD (gt)

⇒ I là trung điểm của AD

Lại có:

H là trung điểm của DC (gt)

⇒ IH là đường trung bình của ∆ACD

⇒ IH // AC và IH = AC : 2

Do G là trung điểm của AC (gt)

⇒ CG = AC : 2

⇒ IH = CG = AC : 2

Do IH // AC (cmt)

⇒ IH // AG

Tứ giác IHCG có:

IH // CG (cmt)

IH = CG (cmt)

⇒ IHCG là hình bình hành

c) Do E là hình chiếu của D lên AB (gt)

⇒ DE ⊥ AB

Mà AC ⊥ AB (cmt)

⇒ DE // AC

⇒ DK // AC

Tứ giác ADKC có:

DK // AC (cmt)

DK = AC (gt)

⇒ ADKC là hình bình hành

⇒ CK // AD

d) Do IH // CG (cmt)

⇒ IH // AC

Mà AC ⊥ AB (cmt)

⇒ IH ⊥ AB

⇒ HI là đường cao của ∆HAB

Do AD là đường cao của ∆ABC (gt)

⇒ AD ⊥ BC

⇒ AD ⊥ BH

⇒ AD là đường cao của ∆HAB

∆HAB có:

HI là đường cao (cmt)

AD là đường cao thứ hai (cmt)

Mà I là giao điểm của HI và AD

⇒ I là giao điểm của ba đường cao của ∆HAB

⇒ I là trực tâm của ∆HAB

a) 9x²(2x - 3) = 0

9x² = 0 hoặc 2x - 3 = 0

*) 9x² = 0

x² = 0

x = 0

*) 2x - 3 = 0

2x = 3

Vậy:

b; (4\(x+2\))(\(x^2\) + 1) = 0

     \(x^2\) ≥ 0 ⇒ \(x^2\) + 1 ≥ 1 ∀ \(x\)

 ⇒   4\(x+2\) = 0  ⇒ 4\(x=-2\) ⇒ \(x=-\dfrac{1}{2}\)

Vậy \(x=-\dfrac{1}{2}\) 

A  =5 + 5² + 5³ + ... + 5¹⁰⁰

A ⋮ 1; 5 ; A (A > 5)

Vậy A là hợp số

b; A = 5 + 5² + 5³ + ... + 5¹⁰⁰

   A =  5 + 5²(1 + 5  + 5² + ... + 5⁹⁸)

 ⇒  A \(⋮\) 5; A không chia hết cho 5². Vậy A không phải là số chính phương vì số chính phương chia hết cho một số nguyên tố thì phải chia hết cho bình phương số nguyên tố đó. 

\(56-22\left(x+3\right)^3=2\)

=>\(22\left(x+3\right)^3=56-2=54\)

=>\(\left(x+3\right)^3=\dfrac{54}{22}=\dfrac{27}{11}\)

=>\(x+3=\dfrac{3}{\sqrt[3]{11}}\)

=>\(x=\dfrac{3\sqrt[3]{121}}{121}-3=\dfrac{3\sqrt[3]{121}-363}{121}\)

Chép đúng đề chưa em, lớp sáu chưa học căn em ơi?

2^\(2+x\) + 2^\(x\)  = 80

2^\(x\).2² + 2^\(x\) = 80

2\(^x\).(2² + 1) =  80

2\(^x\).(4 + 1) = 80

2\(^x\).5 = 80

2\(^x\)     = 80 : 5

2\(^x\)     = 16

2\(^x\)     = 2⁴

\(x=4\)

Vậy \(x=4\)

\(2^{x+2}+2^x=80\)

=>\(4\cdot2^x+2^x=80\)

=>\(5\cdot2^x=80\)

=>\(2^x=\dfrac{80}{5}=16=2^4\)

=>x=4

`a,` Mỗi ngày, tổng số tiền góp của cả hai bạn là:

`5000 . 2 = 10000 (` đồng `)`

Sau `10` ngày, tổng số tiền góp được là:

`10000 . 10 = 100000 (` đồng `)`

`b,` Ngày thứ `2`, mỗi bạn góp `5000` đồng.

Ngày thứ `3`, mỗi bạn góp gấp đôi ngày trước là `5000 . 2 = 10000 (` đồng `)`

Ngày thứ `4`, mỗi bạn góp gấp đôi ngày trước là: `10000 . 2 = 20000 (` đồng `)`

Ngày thứ `5`, mỗi bạn góp gấp đôi ngày trước là: `20000 . 2 = 40000 (` đồng `)`

Biểu thức tổng số tiền của mộtbạn sau ngày thứ năm là: `5000 . 2^0 + 5000 . 2^1 + 5000 . 2^2 + 5000 .  2^3 + 5000 . 2^4 (` đồng `)`

Biểu thức tổng số tiền của cả hai bạn sau ngày thứ năm là:`2 . [5000 . (2^0 + 2^1 + 2^2 + 2^3 + 2^4)] (` đồng `)`